题目内容

已知sin2α=
1
3
，则cos2（α-
π
4
）=（　　）
A、
3
4
B、
2
3
C、
4
5
D、
5
6
考点：二倍角的余弦,三角函数的化简求值
专题：三角函数的求值
分析：利用二倍角的余弦公式化简后，由诱导公式化简即可求值．
解答： 解：∵sin2α=
1
3
，
∴cos2（α-
π
4
）=
1+cos(2α-
π
2
)
2
=
1+sin2α
2
=
1+
1
3
2
=
2
3
．
故选：B．
点评：本题主要考查了二倍角的余弦公式，诱导公式的应用，属于基本知识的考查．
练习册系列答案
相关题目
某市环保所对市中心每天环境污染情况进行调查研究后，得出一天中环境综合污染指数f（x）与时间（小时）的关系为f（x）=|
1
2
sin（
π
32
x）+
1
3
-a|+2a，x∈[0，24]，其中a为气象有关的参数，且a∈[0，1]，若用每天f（x）的最大值为当天的综合污染指数，并记作M（a）．
（Ⅰ）令t=
1
2
sin（
π
32
x），x∈[0，24]，求t的取值范围；并求函数M（a）关于a的解析式；
（Ⅱ）为加强对环境污染的整治，市政府规定每天的综合污染指数不得超过2，试问目前市中心的综合污染指数是否超标？
已知集合A={x|log
1
2
（x+2）＞-3}，B={x|-3≤x≤5}，C={x|m+1≤x≤2m-1}．
（1）求集合A∩B；
（2）若C⊆（A∩B），求实数m的取值范围．
已知函数f（x）=
5-x+4x
2
-
|5-x-4x|
2
，则f（x）的递增区间为
 
，函数g（x）=f（x）-
5
的零点个数为
 
个．
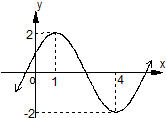已知简谐运动f（x）=Asin（ωx+φ），（|φ|＜
π
2
）的部分图象如右图示，
则该简谐运动的最小正周期和初相φ分别为（　　）
A、T=6，φ=
π
6
B、T=6，φ=
π
3
C、T=6，φ=
π
6
D、T=6，φ=
π
3
已知复数z=
1+i
2+i
（其中i是虚数单位），则复数z在坐标平面内对应的点在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
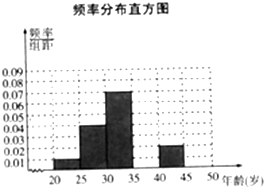为调查市民对汽车品牌的认可度，在秋季车展上，从有意购车的500名市民中，随机抽样100名市民，按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2
频率分布表Ⅰ
分组（单位：岁）频数频率
[20，25]50.05
[25，30]200.20
[30，35]①0.350
[35，40]30②
[40，45]100.10
合计1001.000
（1）频率分布表中的①②位置应填什么数？并补全频率分布直方图，再根据频率分布直方图统计这500名志愿者得平均年龄；
（2）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加的宣传活动，再从这20名中选取2名志愿者担任主要发言人．记这2名志愿者中“年龄低于30岁”的人数为X，求X的分布列及数学期望．
函数y=
sinx
的定义域为（k∈Z）（　　）
A、[2kπ，π+2kπ]
B、（2kπ，π+2kπ）
C、[π+2kπ，2π+2kπ]
D、（π+2kπ，2π+2kπ）
已知|
a
|=2，|
b
|=3，
a
，
b
的夹角为60°，则|2
a
-
b
|=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网