题目内容
若双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1有公共点,则此双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、[
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先根据双曲线方程求得双曲线的渐近线,进而利用圆心到渐近线的距离小于等于半径求得a和b的关系,进而利用c2=a2+b2求得a和c的关系,则双曲线的离心率可求.
解答:
解:∵双曲线渐近线为bx±ay=0,与圆(x-2)2+y2=1有公共点,
∴圆心到渐近线的距离小于等于半径,即
≤1
∴3b2≤a2,
∴c2=a2+b2≤
a2,
∴e=
≤
∵e>1
∴1<e≤
.
故选:B.
∴圆心到渐近线的距离小于等于半径,即
| 2b | ||
|
∴3b2≤a2,
∴c2=a2+b2≤
| 4 |
| 3 |
∴e=
| c |
| a |
2
| ||
| 3 |
∵e>1
∴1<e≤
2
| ||
| 3 |
故选:B.
点评:本题主要考查了双曲线的简单性质,直线与圆的位置关系,点到直线的距离公式等,属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
阅读如图所示的程序框图,输出的结果S的值为( )


| A、0 | ||||
B、
| ||||
C、
| ||||
D、-
|
过空间任意一点引三条直线,它们所确定的平面个数是( )
| A、1 | B、2 | C、3 | D、1或3 |
当x∈[a,b]时,函数f(x)=|x+1|+|3-x|的最大值为10,最小值4,则b-a的范围是( )
| A、[2,8] |
| B、[3,7] |
| C、[3,10] |
| D、[2,10] |
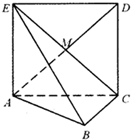 如图,正方形 ACD E所在的平面与平面 A BC垂直,M是C E和 AD的交点,AC⊥BC,且 AC=BC.
如图,正方形 ACD E所在的平面与平面 A BC垂直,M是C E和 AD的交点,AC⊥BC,且 AC=BC.