题目内容
正方体的棱长为a，P为B1C1的中点，A1C1与PD1交于M，B1C与PB交于N，求证：MN⊥A1C1，MN⊥B1C，并求MN的长．
考点：点、线、面间的距离计算
专题：空间位置关系与距离,空间向量及应用
分析：分别以CB，CD，CC1为x，y，z轴建立空间直角坐标系，写出
，
，
的坐标，运用向量的数量积为0，判断直线垂直，我iu向量的模求线段的长度．
| MN |
| A1C1 |
| B1C |
解答：
证明：如图
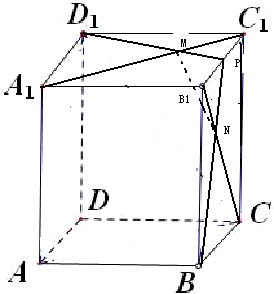
分别以CB，CD，CC1为x，y，z轴建立空间直角坐标系，正方体的棱长为a，P为B1C1的中点，
所以C（0，0，0），P（
a，0，a），M（
a，
a，a），N（
a，0，
a），A1（a，a，a），C1（0，0，a），B1（a，0，a），
所以
=（
a，-
a，-
a），
=（-a，-a，0），
=（-a，0，-a），
所以
•
=-
a2+
a2+0=0，
•
=-
a2+0+
a2=0，|
|=
=
a；
所以MN⊥A1C1，MN⊥B1C，MN=
a．
分别以CB，CD，CC1为x，y，z轴建立空间直角坐标系，正方体的棱长为a，P为B1C1的中点，
所以C（0，0，0），P（
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
所以
| MN |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| A1C1 |
| B1C |
所以
| MN |
| A1C1 |
| 1 |
| 3 |
| 1 |
| 3 |
| MN |
| B1C |
| 1 |
| 3 |
| 1 |
| 3 |
| MN |
| 1 |
| 3 |
| a2+a2+a2 |
| ||
| 3 |
所以MN⊥A1C1，MN⊥B1C，MN=
| ||
| 3 |
点评：本题考查了线线垂直的判定以及线段长度的求法；本题借助于空间向量的数量积以及模求直线垂直和线段的长度；关键是适当建立坐标系，正确找出向量的坐标，正确运算．
练习册系列答案
相关题目
sin660°等于（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设全集R，若集合A={x||x-2|≤3}，B={x||2x-1|＞1}，则∁R（A∩B）为（ ）
| A、{x|x≤1或x＞5} |
| B、{x|x≤-1或x＞5} |
| C、{x|1＜x≤5} |
| D、{x|-1≤x≤5} |
如图，正方体的棱长是a，C，D分别是两条棱的中点．