题目内容
已知 分别是
分别是 中角
中角 的对边,且
的对边,且 ,
,
⑴求角 的大小;⑵若
的大小;⑵若 ,求
,求 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)利用正弦定理的变式 代入原式的两边可得边的关系,再用余弦定理求解即可;(2)利用正弦定理的变式
代入原式的两边可得边的关系,再用余弦定理求解即可;(2)利用正弦定理的变式 代入
代入 左右两边,化为角的关系求解.此两小题充分考查了正弦定理边化角,角化边的功能.
左右两边,化为角的关系求解.此两小题充分考查了正弦定理边化角,角化边的功能.
试题解析:(1)由已知条件及正弦定理,得: ,则
,则 ,根据余弦定理的推论,得
,根据余弦定理的推论,得 ,又
,又 ,所以
,所以 .
.
(2)因为 ,由正弦定理,得
,由正弦定理,得 ,且
,且 ,所以有
,所以有 ,整理得:
,整理得: ,从而得:
,从而得: .
.
考点:1,正弦定理,余弦定理及其变;2,三角变换基本公式,如两角差的正弦公式,商数关系.

练习册系列答案
相关题目
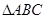 的内角
的内角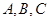 的对边分别
的对边分别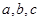 且
且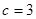 ,
,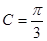 ,若
,若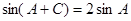 ,求
,求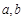 的值。
的值。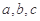 ,且,,.
,且,,. 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且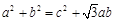 .
.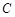 的值;(2)若
的值;(2)若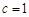 ,求
,求 的取值范围.
的取值范围. 的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.
的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.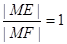 时,试问x的值为多少?(2)求
时,试问x的值为多少?(2)求 的取值范围.
的取值范围. ≥0对一切实数
≥0对一切实数 恒成立.
恒成立. 中,
中, 是三个内角
是三个内角 的对边,关于
的对边,关于 的不等式
的不等式
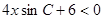 的解集是空集.
的解集是空集. 的最大值;
的最大值; ,
, ,求当角
,求当角 的值.[
的值.[ 是三内角对应的三边,已知
是三内角对应的三边,已知 .(1)求角A的大小;(2)若
.(1)求角A的大小;(2)若 =
=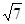 ,且△ABC的面积为
,且△ABC的面积为 ,求
,求 的值.
的值.