题目内容
在△ABC中,∠A,∠B,∠C所对的边分别是a、b、c,不等式 ≥0对一切实数
≥0对一切实数 恒成立.
恒成立.
(1)求cosC的取值范围;
(2)当∠C取最大值,且△ABC的周长为6时,求△ABC面积的最大值,并指出面积取最大值时△ABC的形状.
(1)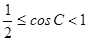 ;(2)
;(2)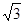 。
。
解析试题分析:(1) 需对 分情况讨论,cosC≠0时,则为一元二次不等式恒成立问题,则需
分情况讨论,cosC≠0时,则为一元二次不等式恒成立问题,则需 ;
;
(2)因为S△ABC=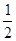
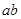
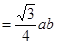 ,只需求
,只需求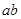 的最大值,再由余弦定理的应用及基本不等式去求。
的最大值,再由余弦定理的应用及基本不等式去求。
(1)当cosC=0时,sinC=1,原不等式即为4x+6≥0对一切实数x不恒成立.
当cosC≠0时,应有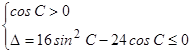
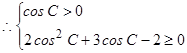 ,解得
,解得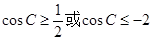 (舍去)
(舍去)
∵C是△ABC的内角, ∴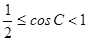
(2)∵0<C<π,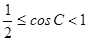
∴∠C的最大值为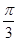 , 此时
, 此时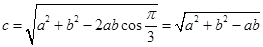 ,
,
∴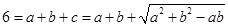 ≥
≥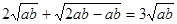 ,
,
∴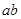 ≤4(当且仅当a=b时取“=”),
≤4(当且仅当a=b时取“=”),
∴S△ABC=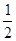
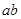
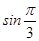 ≤
≤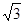 (当且仅当a=b时取“=”),
(当且仅当a=b时取“=”),
此时,△ABC面积的最大值为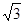 ,△ABC为等边三角形。
,△ABC为等边三角形。
考点:(1)一元二次不等式的解法;(2)余弦定理的应用;(3)利用基本不等式求最值。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 cosx(m>0)的最大值为2.
cosx(m>0)的最大值为2.  角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积. 三个内角
三个内角 ,
, ,
, 的对边分别为
的对边分别为 ,
,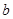 ,
,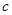 ,且
,且 ,
, ,
, ,求
,求 分别是
分别是 中角
中角 的对边,且
的对边,且 ,
, 的大小;⑵若
的大小;⑵若 ,求
,求 的值.
的值. 。
。 ,函数
,函数 .
. 的对称中心;
的对称中心;  中,
中, 分别是角
分别是角 对边,且
对边,且 ,且
,且 ,求
,求 的取值范围.
的取值范围.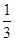 ,求B.
,求B.
 、
、 是两个小区所在地,
是两个小区所在地, 的垂直距离分别为
的垂直距离分别为
 ,
,
 ,在
,在 、
、 、
、 ,在
,在 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得