Question

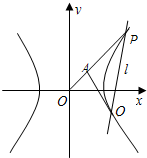已知椭圆C₁：

x2

t

+y²=36（t＞0）的两条准线与双曲线C₂：5x²-y²=36的两条准线所围成的四边形面积为12

6

，直线l与双曲线C₂的右支相交于P、Q两点（其中P点在第一象限），线段OP与椭圆C₁交于点A，O为坐标原点（如图所示）
（Ⅰ）求实数t的值；
（Ⅱ）若

OP

=3

OA

，△PAQ的面积S=-26•tan∠PAQ，求
（1）线段AP的长，
（2）直线l的方程．

Answer 1

考点：直线与圆锥曲线的关系,直线的一般式方程与直线的平行关系

专题：圆锥曲线中的最值与范围问题

分析：（I）由双曲线C₂：5x²-y²=36可得两条准线方程为x=±

a2

c

=

30

5

．由椭圆C₁：

x2

t

+y²=36（t＞0）化为

x2

36t

+

y2

36

=1，可得C₁准线方程为y=±

6

1-t

．利用12

6

=2×

30

5

×2×

6

1-t

，解得t即可得出．
（II）（1）由（I）可得C₁：5x²+y²=36，C₂：5x²-y²=36，设P（x₁，y₁），Q（x₂，y₂），由

OP

=3

OA

得A(

x1

3

，

y1

3

)，把P，A分别代入双曲线与椭圆的方程解出即可得出．
（2）由△PAQ的面积S=-26•tan∠PAQ=

1

2

|AP||AQ|sin∠PAQ，可得|AQ|cos∠PAQ=-

13

5

，由

AP

•

AQ

=|

AP

||

AQ

|cos∠PAQ可得

AP

•

AQ

=-52．利用数量积运算及其Q在双曲线C₂上，联立解得即可．

解答： 解：（I）双曲线C₂：5x²-y²=36化为：

x2

36 5

-

y2

36

=1，可得a2=

36

5

，b²=36，c²=a²+b²=

216

5

．
∴两条准线方程为x=±

a2

c

=

30

5

．
椭圆C₁：

x2

t

+y²=36（t＞0）化为

x2

36t

+

y2

36

=1，
由题意可知t＜1，可得C₁准线方程为y=±

6

1-t

．
由12

6

=2×

30

5

×2×

6

1-t

，解得t=

1

5

＜1满足题意．
故t=

1

5

．
（II）（1）由（I）可得C₁：5x²+y²=36，C₂：5x²-y²=36，
设P（x₁，y₁），Q（x₂，y₂），则5

x

2 1

-

y

2 1

=36，①
∵

OP

=3

OA

得A(

x1

3

，

y1

3

)，
代入椭圆方程得5

x

2 1

+

y

2 1

=36×9     ②
联立①得x₁=6，y₁=12，
故P（6，12），A（2，4），有|AP|=4

5

．
（2）由△PAQ的面积S=-26•tan∠PAQ=

1

2

|AP||AQ|sin∠PAQ，
∴|AQ|cos∠PAQ=-

13

5

，
由

AP

•

AQ

=|

AP

||

AQ

|cos∠PAQ可得

AP

•

AQ

=-52．
即4（x₂-2）+8（y₂-4）=-52 ③
又Q在双曲线C₂上有5

x

2 2

-

y

2 2

=36④
联立③④得x₂=3，y₂=-3，
由P（6，12），Q（3，-3）得直线l方程为：5x-y-18=0．

点评：本题考查了椭圆与双曲线的标准方程及其性质、向量的坐标运算及其数量积运算、三角形的面积计算公式、矩形的面积计算公式、直线的方程，考查了推理能力与计算能力，属于难题．