题目内容
设集合A={x|x2+2x-3＜0}，B={x|log2|x|＜1}，则A∩B等于（ ）
| A、（-3，0）∪（0，1） |
| B、（-2，0）∪（0，1） |
| C、（-1，0）∪（0，1） |
| D、（-2，1） |
考点：交集及其运算
专题：集合
分析：求出集合A，B，利用集合的基本运算即可得到结论．
解答：
解：A={x|x2+2x-3＜0}={x|-3＜x＜1}，
B={x|log2|x|＜1}={x||x|＜2且x≠0}={x|-2＜x＜2且x≠0}，
则A∩B={x|-2＜x＜1且x≠0}，
故选：B
B={x|log2|x|＜1}={x||x|＜2且x≠0}={x|-2＜x＜2且x≠0}，
则A∩B={x|-2＜x＜1且x≠0}，
故选：B
点评：本题主要考查集合的基本运算，利用不等式的解法解不等式是解决本题的关键．
练习册系列答案
相关题目
若复数z=i+i2014，则复数
+
（i为虚数单位）在复平面内对应的点所在象限为（ ）
. |
| z |
| 10 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数y=loga（3x-2）+1（a＞0且a≠1）恒过定点（ ）
| A、（2，1） |
| B、（1，0） |
| C、（1，1） |
| D、（3，1） |
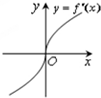已知定义在R上的函数f（x）满足f（-1）=f（3）=1，f′（x）为f（x）的导函数，且导函数y=f′（x）的图象如图所示．则不等式f（x）＜1的解集是（ ）| A、（-1，0） |
| B、（-1，3） |
| C、（0，3） |
| D、（-∞，-1）（3，+∞） |
已知复数z=
，则
的虚部为（ ）
| 1+3i |
| 1-i |
. |
| z |
| A、l | B、2 | C、-2 | D、-1 |
某学员在一次射击测试中射靶10次，命中环数如：7，8，7，9，5，4，9，10，7，4则平均命中环数和命中环数的标准差为（ ）
| A、7，2 | B、7，4 |
| C、6，2 | D、6，4 |
若定义域为区间（-2，-1）的函数f（x）=log（2a-3）（x+2），满足f（x）＜0，则实数a的取值范围是（ ）
A、（
| ||
| B、（2，+∞） | ||
C、（
| ||
D、（1，
|