题目内容
已知函数f(x)=x3+(a-1)x2是奇函数,则函数g(x)=
的定义域是 .
| ||
| x-a |
考点:函数奇偶性的性质,函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数奇偶性的性质求出a,即可.
解答:
解:∵f(x)=x3+(a-1)x2是奇函数,
∴a-1=0,解得a=1,
则g(x)=
=
,
要使函数有意义,则
,
即
,
解得0≤x<1,
即函数的定义域为[0,1),
故答案为:[0,1)
∴a-1=0,解得a=1,
则g(x)=
| ||
| x-a |
| ||
| x-1 |
要使函数有意义,则
|
即
|
解得0≤x<1,
即函数的定义域为[0,1),
故答案为:[0,1)
点评:本题主要考查函数奇偶性的应用以及函数定义域的求解,根据条件求出a是 解决本题的关键..

练习册系列答案
相关题目
已知集合A={-1,0},则集合A的子集有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
正实数a,b满足a+2b=30,则ab的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
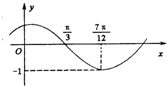 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|