题目内容
10.已知{an}是公差为2的等差数列,数列{bn}满足b1=1,b2=$\frac{1}{2}$,且对一切n∈N*恒有anbn+1+bn+1=nbn.(Ⅰ)求{an}的通项公式;
(Ⅱ)求{bn}的通项公式.
分析 (Ⅰ)令n=1,可得a1=1,结合{an}是公差为2的等差数列,可得{an}的通项公式,
(Ⅱ)将其代入已知条件anbn+1+bn+1=nbn来求{bn}的通项公式;
解答 解:(Ⅰ)∵anbn+1+bn+1=nbn.
当n=1时,a1b2+b2=b1.
∵b1=1,b2=$\frac{1}{2}$,
∴a1=1,
又∵{an}是公差为2的等差数列,
∴an=1+2(n-1)=2n-1,
(Ⅱ)∵anbn+1+bn+1=nbn,
∴(2n-1)bn+1+bn+1=nbn.
化简,得
2bn+1=bn,即$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{1}{2}$,
∴数列{bn}是以1为首项,以$\frac{1}{2}$为公比的等比数列,
∴bn=($\frac{1}{2}$)n-1
点评 本题考查的知识点是数列的递推式,数列的通项公式,难度中档.

练习册系列答案
相关题目
1.观察:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a9+b9=( )
| A. | 28 | B. | 76 | C. | 123 | D. | 199 |
 已知如图是一个空间几何体的三视图.
已知如图是一个空间几何体的三视图.
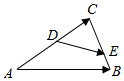 如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.
如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.