题目内容
 已知函数f(x)=x2-4|x|+3,
已知函数f(x)=x2-4|x|+3,(1)画出f(x)的图象;
(2)请根据图象指出函数f(x)的单调递增区间与单调递减区间;(不必证明)
(3)当实数k取不同的值时,讨论关于x的方程x2-4|x|+3=k的实根的个数.
考点:二次函数的性质,函数的图象,根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)先去绝对值,然后根据二次函数、分段函数图象的画法画出函数f(x)的图象;
(2)通过图象即可求得f(x)的单调递增和递减区间;
(3)通过图象即可得到k的取值和对应的原方程实根的个数.
(2)通过图象即可求得f(x)的单调递增和递减区间;
(3)通过图象即可得到k的取值和对应的原方程实根的个数.
解答:
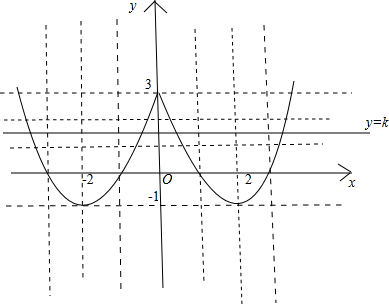 解:(1)f(x)=
解:(1)f(x)=
,所以图象如下:
(2)根据图象便得到f(x)的单调递增区间为[-2,0),[2,+∞);
单调递减区间为(-∞,-2),[0,2);
(3)由图象可看出,当k<-1时,方程实根的个数为0;
当k=-1时,方程实根的个数为2;
当-1<k<3时,方程实根个数为4;
当k=3时,方程实根个数为3;
当k>3时,方程实根个数为2.
 解:(1)f(x)=
解:(1)f(x)=
|
(2)根据图象便得到f(x)的单调递增区间为[-2,0),[2,+∞);
单调递减区间为(-∞,-2),[0,2);
(3)由图象可看出,当k<-1时,方程实根的个数为0;
当k=-1时,方程实根的个数为2;
当-1<k<3时,方程实根个数为4;
当k=3时,方程实根个数为3;
当k>3时,方程实根个数为2.
点评:考查含绝对值函数的处理方法:去绝对值,二次函数、分段函数图象的画法,函数单调性的定义,以及根据图象写出函数的单调区间,数形结合讨论方程实根个数的方法.

练习册系列答案
相关题目
已知全集U=(-1,1),集合A={1,2},B={2,3,4},则(∁UA)∩B=( )
| A、{2} |
| B、{3,4} |
| C、{1,4,5} |
| D、{2,3,4,5} |
在长为6cm的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AC,BC的长,则该矩形面积小于8cm2,的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
P是双曲线
-
=1上一点,F1、F2是双曲线的两个焦点,且|PF1|=17,则|PF2|的值为( )
| x2 |
| 64 |
| y2 |
| 36 |
| A、33 | B、33或1 |
| C、1 | D、25或9 |
在△ABC中,已知a=4,b=4
,A=30°,B为锐角,那么角A,B,C的大小关系为( )
| 3 |
| A、A>B>C |
| B、B>A>C |
| C、C>B>A |
| D、C>A>B |
 在锐角△ABC中,BC=5,sinA=
在锐角△ABC中,BC=5,sinA=