题目内容
20.设x1,x2,…,xn的平均数是$\overline{x}$,标准差是s,则另一组数4x1+1,4x2+1,…,4xn+1的平均数和标准差分别是$4\overline{x}$+1,4s.分析 由E(aξ+b)=aE(ξ)+b,D(aξ+b)=a2D(ξ),利用x1,x2,…,xn的平均数是$\overline{x}$,标准差是s,能求出另一组数4x1+1,4x2+1,…,4xn+1的平均数和标准差.
解答 解:∵x1,x2,…,xn的平均数是$\overline{x}$,标准差是s,
∴另一组数4x1+1,4x2+1,…,4xn+1的平均数为:
$\frac{1}{n}$(4x1+1+4x2+1…+4xn+1)=4×$\frac{1}{n}$(x1+x2+…+xn)+1=4$\overline{x}$+1;
另一组数4x1+1,4x2+1,…,4xn+1的方差为:16s2,
∴另一组数4x1+1,4x2+1,…,4xn+1的标准差; $\sqrt{16{s}^{2}}=4s$.
故答案为:$4\overline{x}$+1,4s.
点评 本题考查平均数、方差的求法,是基础题,解题时要认真审题,注意平均数和方差性质的合理运用.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
14.已知p:a>4,q:方程$\frac{{x}^{2}}{4-a}$-$\frac{{y}^{2}}{1-a}$=1表示双曲线,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
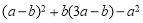 ,其中
,其中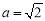 ,
,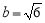 .
.
 的最小正周期为
的最小正周期为 ,则
,则 的值是 .
的值是 .