题目内容
已知函数f（x）=
，则f（f（
））的值是（ ）
|
| 1 |
| 2 |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、4 |
考点：函数的值
专题：函数的性质及应用
分析：利用分段函数的性质求解．
解答：
解：∵函数f（x）=
，
∴f（
）=log2
=-1，
f（f（
））=f（-1）=3-1+1=
．
故选：B．
|
∴f（
| 1 |
| 2 |
| 1 |
| 2 |
f（f（
| 1 |
| 2 |
| 4 |
| 3 |
故选：B．
点评：本题考查函数值的求法，是基础题，解题时要注意分段函数的性质的合理运用．
练习册系列答案
相关题目
已知直线y=kx与曲线y=lnx有交点，则k的最大值是（ ）
| A、e | ||
| B、-e | ||
C、
| ||
D、-
|
若a，b都是实数，则“a-b＞0”是“a2-b2＞0”的（ ）
| A、既不充分也不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、充分而不必要条件 |
函数f（x）=（3-x）ex的单调递增区间是（ ）
| A、（-∞，2） |
| B、（0，3） |
| C、（1，4） |
| D、（2，+∞） |
从5名男生和3名女生中选出3名志愿者，其中男生和女生都至少有1人被选中，则不同的选法方案共有（ ）
| A、45种 | B、10种 |
| C、9种 | D、46种 |
已知x＞0，y＞0，且2x+y=1，则
+
的最小值为（ ）
| 1 |
| x |
| 1 |
| y |
| A、3 | ||
B、2+3
| ||
C、3+2
| ||
D、2-3
|
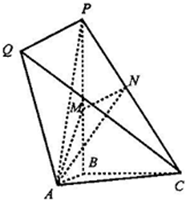如图所示的几何体中，PB⊥面ABC，PQ∥AB，PQ=PB=1；Rt△ABC中，∠ABC=90°，AB=BC=