题目内容
盒中有10只螺丝钉,其中有3只是不合格的,现从盒中随机地抽取4个,那么恰有两只不合格的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:计算题,概率与统计
分析:先确定符合古典概型,再利用概率公式求解.
解答:
解:由题意,符合古典概型,
恰有两只不合格的概率P=
=
.
故选B.
恰有两只不合格的概率P=
| ||||
|
| 3 |
| 10 |
故选B.
点评:本题考查了古典概型概率的求法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设直线l经过点M(1,5)、倾斜角为
,则直线l的参数方程可为( )
| π |
| 3 |
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|
把正整数按图所示的规律排序,则从2008到2010的箭头方向依次为( )


A、 |
B、 |
C、 |
D、 |
在区间[0,10]中任意取一个数,则它与4之和大于10的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线y=x3与直线y=x所围成图形的面积为( )
A、
| ||
B、
| ||
C、2
| ||
D、2
|
若9n+Cn+11•9n-1+…+Cn+1n-1•9+Cn+1n是11的倍数,则自然数n为( )
| A、奇数 | B、偶数 |
| C、3的倍数 | D、被3除余1的数 |
已知曲线y=
x2-2上一点P(1,-
),则过点P的切线的方程是( )
| 1 |
| 2 |
| 3 |
| 2 |
| A、2x-2y-5=0 |
| B、2x+y+1=0 |
| C、2x-2y+5=0 |
| D、2x-y+1=0 |
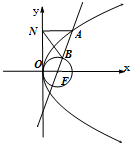 如图,抛物线C:y2=2px(p>0)的焦点为F,A为C上的点,以F为圆心,
如图,抛物线C:y2=2px(p>0)的焦点为F,A为C上的点,以F为圆心,