题目内容
14.已知圆C:x2+y2=4,点P为直线x+2y-9=0上一动点,过点P向圆C引两条切线PA、PB,A、B为切点,则直线AB经过定点( )| A. | $(\frac{4}{9},\frac{8}{9})$ | B. | $(\frac{2}{9},\frac{4}{9})$ | C. | (2,0) | D. | (9,0) |
分析 根据题意设P的坐标为P(9-2m,m),由切线的性质得点A、B在以OP为直径的圆C上,求出圆C的方程,将两个圆的方程相减求出公共弦AB所在的直线方程,再求出直线AB过的定点坐标.
解答 解:因为P是直线x+2y-9=0的任一点,所以设P(9-2m,m),
因为圆x2+y2=4的两条切线PA、PB,切点分别为A、B,
所以OA⊥PA,OB⊥PB,
则点A、B在以OP为直径的圆上,即AB是圆O和圆C的公共弦,
则圆心C的坐标是($\frac{9-2m}{2}$,$\frac{m}{2}$),且半径的平方是r2=$\frac{(9-2m)^{2}+{m}^{2}}{4}$,
所以圆C的方程是(x-$\frac{9-2m}{2}$)2+(y-$\frac{m}{2}$)2=$\frac{(9-2m)^{2}+{m}^{2}}{4}$,①
又x2+y2=4,②,
②-①得,(2m-9)x-my+4=0,即公共弦AB所在的直线方程是:(2m-9)x-my+4=0,
即m(2x-y)+(-9x+4)=0,
由$\left\{\begin{array}{l}{2x-y=0}\\{-9x+4=0}\end{array}\right.$得x=$\frac{4}{9}$,y=$\frac{8}{9}$,
所以直线AB恒过定点($\frac{4}{9}$,$\frac{8}{9}$),
故选A.
点评 本题考查了直线和圆的位置关系,圆和圆的位置关系,圆的切线性质,以及直线过定点问题,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
2.函数f(x)=(3-x2)•ln|x|的大致图象为( )
| A. | 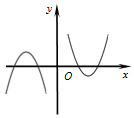 | B. | 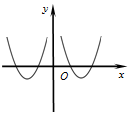 | C. |  | D. | 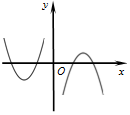 |
3.已知$f(x)=\frac{lnx}{x}$,则( )
| A. | f(2)>f(e)>f(3) | B. | f(3)>f(e)>f(2) | C. | f(3)>f(2)>f(e) | D. | f(e)>f(3)>f(2) |
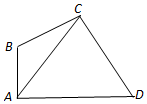 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,DC=$\frac{{4\sqrt{7}}}{5}$
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,DC=$\frac{{4\sqrt{7}}}{5}$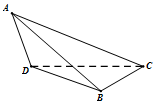 如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.
如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.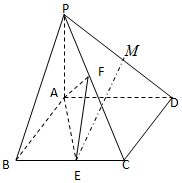 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点.