题目内容
19.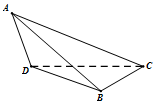 如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.
如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.(Ⅰ)求证:AC⊥BD;
(Ⅱ)求D点到平面ABC的距离.
分析 (Ⅰ)取BD中点M,连AM、CM,证明BD⊥面ACM,即可证明AC⊥BD;
(Ⅱ)证明面ABCE⊥面DEC,过D作DF⊥EC,交EC于F,DF即为D点到平面ABC的距离.
解答 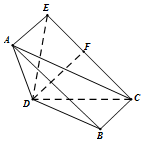 (Ⅰ)证明:取BD中点M,连AM、CM
(Ⅰ)证明:取BD中点M,连AM、CM
∵AD=AB
∴AM⊥BD,
又∵DC=CB,
∴CM⊥BD,CM∩AM=M,
∴BD⊥面ACM,AC?面ACM,
∴BD⊥AC …(6分)
(Ⅱ)过A作AE∥BC,AE=BC,连接EC、ED,
则AB∥EC,AB=EC
∵BC⊥AB,
∴BC⊥EC,
又∵BC⊥DC,EC∩DC=C,
∴BC⊥面DEC
∵BC?面ABCE,
∴面ABCE⊥面DEC
过D作DF⊥EC,交EC于F,DF即为所求,
在△DEC中,DE=DC=1,EC=$\sqrt{2}$,
∴DF=$\frac{\sqrt{2}}{2}$ …(12分)
点评 本题考查线面垂直,面面垂直的证明,考查点到平面距离的计算,属于中档题.

练习册系列答案
相关题目
10.设向量$\overrightarrow a=({m,2}),\overrightarrow b=({1,m+1})$,且$\overrightarrow a$与$\overrightarrow b$的方向相反,则实数m的值为( )
| A. | -2 | B. | 1 | C. | -2或1 | D. | m的值不存在 |
14.已知圆C:x2+y2=4,点P为直线x+2y-9=0上一动点,过点P向圆C引两条切线PA、PB,A、B为切点,则直线AB经过定点( )
| A. | $(\frac{4}{9},\frac{8}{9})$ | B. | $(\frac{2}{9},\frac{4}{9})$ | C. | (2,0) | D. | (9,0) |
11.曲线$y=\frac{{{x^2}+4}}{x}$的一条切线l与y=x,y轴三条直线围成三角形记为△OAB,则△OAB外接圆面积的最小值为( )
| A. | $8\sqrt{2}π$ | B. | $8(3-\sqrt{2})π$ | C. | $16(\sqrt{2}-1)π$ | D. | $16(2-\sqrt{2})π$ |
8.已知函数f(x)=e-x-|lnx|的两个零点分别为x1,x2,则( )
| A. | 0<x1x2<1 | B. | x1x2=1 | C. | 1<x1x2<e | D. | x1x2>e |
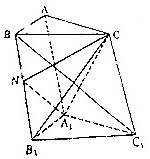 如图,在直三棱柱ABC-A1B1 C1中,AC=2$\sqrt{2}$,AB=BC=BB1=2,N是BB1的中点.
如图,在直三棱柱ABC-A1B1 C1中,AC=2$\sqrt{2}$,AB=BC=BB1=2,N是BB1的中点.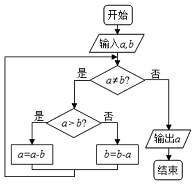 下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为8,12,则输出的a=( )
下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为8,12,则输出的a=( )