题目内容
2．函数f（x）=（3-x2）•ln|x|的大致图象为（ ）| A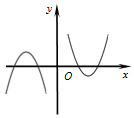． |  | B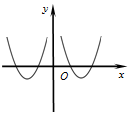． |  | C． |  | D． |  |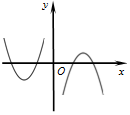
分析 判断函数的奇偶性，排除选项，利用特殊值，判断即可．
解答 解：函数f（x）=（3-x2）•ln|x|是偶函数，排除A，D选项，
（3-x2）•ln|x|=0，当x＞0时，解得x=1，或x=$\sqrt{3}$，是函数f（x）=（3-x2）•ln|x|在x＞0时的两个零点，
当x=$\frac{1}{e}$时，f（$\frac{1}{e}$）=（3-（$\frac{1}{e}$）2）•ln|$\frac{1}{e}$|=$\frac{1}{{e}^{2}}-3$＜0，
可得选项B不正确，
故选：C．
点评 本题考查函数的图象的判断，函数的奇偶性以及特殊值是判断函数的图象的常用方法．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
13．
在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA=AB，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则剩余部分体积与原四棱锥体积的比值为（ ）
在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA=AB，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则剩余部分体积与原四棱锥体积的比值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
10．设向量$\overrightarrow a=（{m，2}），\overrightarrow b=（{1，m+1}）$，且$\overrightarrow a$与$\overrightarrow b$的方向相反，则实数m的值为（ ）
| A． | -2 | B． | 1 | C． | -2或1 | D． | m的值不存在 |
14．已知圆C：x2+y2=4，点P为直线x+2y-9=0上一动点，过点P向圆C引两条切线PA、PB，A、B为切点，则直线AB经过定点（ ）
| A． | $（\frac{4}{9}，\frac{8}{9}）$ | B． | $（\frac{2}{9}，\frac{4}{9}）$ | C． | （2，0） | D． | （9，0） |
11．曲线$y=\frac{{{x^2}+4}}{x}$的一条切线l与y=x，y轴三条直线围成三角形记为△OAB，则△OAB外接圆面积的最小值为（ ）
| A． | $8\sqrt{2}π$ | B． | $8（3-\sqrt{2}）π$ | C． | $16（\sqrt{2}-1）π$ | D． | $16（2-\sqrt{2}）π$ |
12．已知$f（x）=\left\{\begin{array}{l}f（x+1），（x＜1）\\{3^x}\;，\;\;（x≥1）\end{array}\right.$，则f（-1+log35）=（ ）
| A． | 15 | B． | $\frac{5}{3}$ | C． | 5 | D． | $\frac{1}{5}$ |