题目内容
11.化简$\sqrt{{{(π-4)}^2}}+\root{3}{{{{(π-5)}^3}}}$的结果是( )| A. | 2π-9 | B. | 9-2π | C. | -1 | D. | 1 |
分析 根据根式的运算性质$\root{n}{{a}^{n}}=\left\{\begin{array}{l}a,n为奇数\\ \left|a\right|,n为偶数\end{array}\right.$,可得答案.
解答 解:$\sqrt{{{(π-4)}^2}}+\root{3}{{{{(π-5)}^3}}}$=|π-4|+π-5=4-π+π-5=-1,
故选:C
点评 本题考查的知识点是根式的化简和计算,熟练掌握$\root{n}{{a}^{n}}=\left\{\begin{array}{l}a,n为奇数\\ \left|a\right|,n为偶数\end{array}\right.$,是解答的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
1. 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),f(x)的部分图象如图示,则关于y=f(x)错误的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),f(x)的部分图象如图示,则关于y=f(x)错误的是( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),f(x)的部分图象如图示,则关于y=f(x)错误的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),f(x)的部分图象如图示,则关于y=f(x)错误的是( )| A. | 最小正周期为π | |
| B. | 向右平移$\frac{π}{6}$个单位得到函数y=sin(2x-$\frac{π}{6}$) | |
| C. | 在区间[0,$\frac{π}{2}$]上的值域为[-$\frac{1}{2},\frac{1}{2}$] | |
| D. | 向左平移$\frac{π}{6}$个单位得到的图象关于y轴对称 |
19.已知定义在R上的奇函数f(x)满足f(x-2)=-f(x),则f(2006)的值为( )
| A. | 2006 | B. | 1003 | C. | 0 | D. | 不确定 |
6.下列命题中,正确是( )
| A. | 两个向量相等,则它们的起点相同,终点也相同 | |
| B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| C. | 四边形ABCD中,一定有$\overrightarrow{AB}$=$\overrightarrow{DC}$ | |
| D. | 若$\overrightarrow{m}$=$\overrightarrow{n}$,$\overrightarrow{n}$=$\overrightarrow{p}$,则$\overrightarrow{m}$=$\overrightarrow{p}$ |
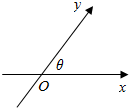 如图,数轴x,y的交点为O,夹角为θ,与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1},\overrightarrow{e_2}$.由平面向量基本定理,对于平面内的任一向量$\overrightarrow{OP}$,存在唯一的有序实数对(x,y),使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,我们把(x,y)叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标).
如图,数轴x,y的交点为O,夹角为θ,与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1},\overrightarrow{e_2}$.由平面向量基本定理,对于平面内的任一向量$\overrightarrow{OP}$,存在唯一的有序实数对(x,y),使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,我们把(x,y)叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标). 如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是$\frac{{\sqrt{10}}}{2}$.
如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是$\frac{{\sqrt{10}}}{2}$.