题目内容
4.已知函数$f(x)=lg(\sqrt{1+4{x^2}}-2x)+1$,则f(3)+f(-3)=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 由已知得f(3)+f(-3)=lg($\sqrt{1+36}-6$)+1+lg($\sqrt{1+36}+6$)+1=lg1+2,由此能求出结果.
解答 解:∵函数$f(x)=lg(\sqrt{1+4{x^2}}-2x)+1$,
∴f(3)+f(-3)=lg($\sqrt{1+36}-6$)+1+lg($\sqrt{1+36}+6$)+1
=lg1+2
=2.
故选:D.
点评 本题考查函数值的求法,考查推理论证能力、运算求解能力,考查化归与转化思想,函数与方程思想,是基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
14. 如图在正方体ABCD-A1B1C1D1中,P是上底面A1B1C1D1内一动点,PM垂直AD于M,PM=PB,则点P的轨迹为( )
如图在正方体ABCD-A1B1C1D1中,P是上底面A1B1C1D1内一动点,PM垂直AD于M,PM=PB,则点P的轨迹为( )
 如图在正方体ABCD-A1B1C1D1中,P是上底面A1B1C1D1内一动点,PM垂直AD于M,PM=PB,则点P的轨迹为( )
如图在正方体ABCD-A1B1C1D1中,P是上底面A1B1C1D1内一动点,PM垂直AD于M,PM=PB,则点P的轨迹为( )| A. | 线段 | B. | 椭圆一部分 | C. | 抛物线一部分 | D. | 双曲线一部分 |
16.圆的任何一对平行切线间的距离总是相等的,即圆在任意方向都有相同的宽度,具有这种性质的曲线可称为“等宽曲线”.事实上存在着大量的非圆等宽曲线,以工艺学家鲁列斯( Reuleaux)命名的鲁列斯曲边三角形,就是著名的非圆等宽曲线.它的画法(如图1):画一个等边三角形ABC,分别以A,B,C为圆心,边长为半径,作圆弧$\widehat{BC},\widehat{CA},\widehat{AB}$,这三段圆弧围成的图形就是鲁列斯曲边三角形.它的宽度等于原来等边三角形的边长.等宽曲线都可以放在边长等于曲线宽度的正方形内(如图2).

在图2中的正方形内随机取一点,则这一点落在鲁列斯曲边三角形内的概率为( )

在图2中的正方形内随机取一点,则这一点落在鲁列斯曲边三角形内的概率为( )
| A. | $\frac{π}{8}$ | B. | $\frac{{2π-3\sqrt{3}}}{4}$ | C. | $\frac{{π-\sqrt{2}}}{2}$ | D. | $\frac{{π-\sqrt{3}}}{2}$ |
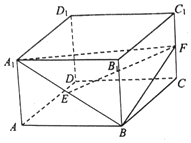 如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.
如图,在四棱柱ABCD-A1B1C1D1中,点E,F分别为A1B,C1C的中点.