题目内容
9.已知函数f(x)=|2x+1|+|2x-1|.(1)求证:f(x)的最小值等于2;
(2)若对任意实数a和b,$|{2a+b}|+|a|-\frac{1}{2}|{a+b}|f(x)≥0$,求实数x的取值范围.
分析 (1)利用绝对值不等式的性质,证明f(x)的最小值等于2;
(2)若对任意实数a和b,$|{2a+b}|+|a|-\frac{1}{2}|{a+b}|f(x)≥0$,分类讨论,当且仅当$-\frac{1}{2}≤x≤\frac{1}{2}$时,f(x)=2.,即可求实数x的取值范围.
解答 (1)证明:∵|2x+1|+|2x-1|=|2x+1|+|1-2x|≥|(2x+1)+1-2x|=2,∴f(x)≥2.
当且仅当(2x+1)(1-2x)≥0时“=”成立,即当且仅当$-\frac{1}{2}≤x≤\frac{1}{2}$时,f(x)=2.
∴f(x)的最小值等于2.
(2)解:当a+b=0即a=-b时,$|{2a+b}|+|a|-\frac{1}{2}|{a+b}|f(x)≥0$可转化为2|b|-0•f(x)≥0,
即2|b|≥0成立,∴x∈R.
当a+b≠0时,
∵|2a+b|+|a|=|2a+b|+|-a|≥|(2a+b)-a|=|a+b|,
当且仅当(2a+b)(-a)≥0时“=”成立,即当且仅当(2a+b)a≤0时“=”成立,
∴$\frac{{|{2a+b}|+|a|}}{{|{a+b}|}}≥1$,且当(2a+b)a≤0时,$\frac{{|{2a+b}|+|a|}}{{|{a+b}|}}=1$,
∴$\frac{{|{2a+b}|+|a|}}{{|{a+b}|}}$的最小值等于1,
∵$|{2a+b}|+|a|-\frac{1}{2}|{a+b}|f(x)≥0$,$?\frac{{|{2a+b}|+|a|}}{{|{a+b}|}}≥\frac{1}{2}f(x)$,
∴$\frac{1}{2}f(x)≤1$,即f(x)≤2.
由(1)知f(x)≥2,∴f(x)=2.
由(1)知当且仅当$-\frac{1}{2}≤x≤\frac{1}{2}$时,f(x)=2.
综上所述,x的取值范围是$[-\frac{1}{2},\frac{1}{2}]$.
点评 本题考查绝对值不等式的性质,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案| A. | -3≤m≤3 | B. | -6≤m≤6 | C. | -3≤m≤6 | D. | -6≤m≤0 |
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
| A. | (0,+∞) | B. | (1,+∞) | C. | [0,+∞) | D. | [1,+∞) |
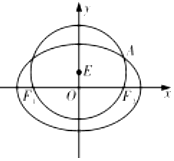 如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.