题目内容
已知命题：“?x∈R，5x+3＞m”为真命题，则m的取值范围是 ．
考点：全称命题
专题：概率与统计
分析：直接利用函数的恒成立，求出函数的最小值，即可得到m的范围．
解答：
解：命题：“?x∈R，5x+3＞m”为真命题，
所以m＜（5x+3）min，∵?x∈R，5x+3＞3，∴m≤3，
m的取值范围是：（-∞，3]．
故答案为：（-∞，3]．
所以m＜（5x+3）min，∵?x∈R，5x+3＞3，∴m≤3，
m的取值范围是：（-∞，3]．
故答案为：（-∞，3]．
点评：本题考查的知识点是命题的真假判断与应用，利用指数函数求出函数的最小值，是解答本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
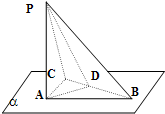如图，BC是Rt△ABC的斜边，过A作△ABC所在平面α垂线AP，连PB、PC，过A作AD⊥BC于D，连PD，那么图中直角三角形的个数
如图，已知正方体ABCD-A1B1C1D1的棱长为a，点M为B1C的中点，点N为A1C1的中点，则MN的长度为函数f（x）=-x3+x2+tx+t在（-1，1）上是增函数，则t的取值范围是（ ）
| A、t＞5 | B、t＜5 |
| C、t≥5 | D、t≤5 |