题目内容
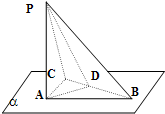如图，BC是Rt△ABC的斜边，过A作△ABC所在平面α垂线AP，连PB、PC，过A作AD⊥BC于D，连PD，那么图中直角三角形的个数考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：利用AP⊥面ABC，Rt△ABC，AD是PD在面ABC内的射影，故由AD⊥BC可得PD⊥BC．
解答：
解：∵BC是Rt△ABC的斜边，
A作△ABC所在平面a垂线AP，AD⊥BC于D，
图中直角三角形有：
△ABC，△PAB，△PAD，△PAC，△ADB，△ADC，△PDB，△PDC 共8个，
故答案：8．
A作△ABC所在平面a垂线AP，AD⊥BC于D，
图中直角三角形有：
△ABC，△PAB，△PAD，△PAC，△ADB，△ADC，△PDB，△PDC 共8个，
故答案：8．
点评：本题考查三垂线定理的应用，以及棱锥的结构特征，体现数形结合的数学思想．
练习册系列答案
相关题目
5名运动员争夺3项比赛冠军（每项比赛无并列冠军），获得冠军的可能种数为（ ）
| A、35 | ||
B、
| ||
C、
| ||
| D、53 |