题目内容
命题“?x≥1,2x≥2”的否定是 .
考点:命题的否定
专题:简易逻辑
分析:直接利用全称命题的否定是特称命题写出结果即可.
解答:
解:因为全称命题的否定是特称命题.所以,命题“?x≥1,2x≥2”的否定是”的否定是?x0∈R,2 x0<2.
故答案为:?x0∈R,2 x0<2.
故答案为:?x0∈R,2 x0<2.
点评:本题考查命题的否定,注意全称命题与特称命题的否定关系,基本知识的考查.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
复数z=1-i,则
+z对应的点所在的象限为( )
| 1 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设全集U=R,集合 A={x|0<x≤2},B={x|x<1},则集合 A∪B=( )
| A、(2,+∞) |
| B、[2,+∞) |
| C、(-∞,2] |
| D、(-∞,1] |
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
|
A、(-3,-
| ||||
B、(-
| ||||
C、(-3,-
| ||||
| D、(-3,-1) |
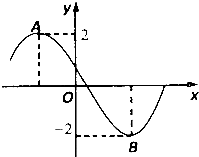 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,