题目内容
8.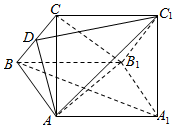 如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C菱形,∠CBB1=60°,AB⊥平面BB1C1C,且D是BC的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C菱形,∠CBB1=60°,AB⊥平面BB1C1C,且D是BC的中点.(1)求证:A1B∥平面ADC1;
(2)若AB=2,求三棱锥B1-ABC体积.
分析 (1)连接A1C,与AC1交于O,连接OD,利用三角形中位线的性质,证明A1B∥OD,利用线面平行的判定定理证明A1B∥平面AC1D;
(2)利用等体积转化法求解三棱锥B1-ABC体积即可.
解答 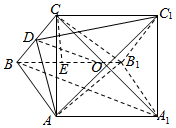 (1)证明:连接A1C,与AC1交于O,连接OD,则O是AC1的中点,
(1)证明:连接A1C,与AC1交于O,连接OD,则O是AC1的中点,
∵D是BC的中点,
∴OD∥A1B,
∵A1B?平面ADC1,OD?平面ADC1,
∴A1B∥平面ADC1;
(2)解:设E是BB1的中点,连结CE,则CE⊥BB1.
∵AB⊥平面BB1C1C,
∴AB⊥CE,
∵AB∩BB1=B,
∴CE⊥平面ABB1A1,且CE=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$.
∴三棱锥B1-ABC体积=三棱锥C-ABB1体积=$\frac{1}{3}{S}_{△AB{B}_{1}}•CE$=$\frac{1}{6}$AB2•CE=$\frac{2\sqrt{3}}{3}$
点评 本题考查几何体的体积的求法,直线与平面平行的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18.对于函数f(x)在定义域内用二分法的求解过程中得到f(2015)<0,f(2016)<0,f(2017)>0,则下述描述正确的是( )
| A. | 函数f(x)在(2015,2016)内不存在零点 | |
| B. | 函数f(x)在(2016,2017)内不存在零点 | |
| C. | 函数f(x)在(2016,2017)内存在零点,并且仅有一个 | |
| D. | 函数f(x)在(2015,2016)内可能存在零点 |
17.已知f(x)是定义在R上的偶函数,且f(2)=8,则f(-2)的值为( )
| A. | -16 | B. | 16 | C. | -8 | D. | 8 |
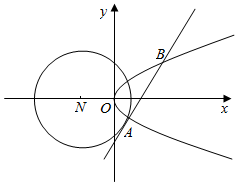 如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.