题目内容
log23log34+lg22+lg2lg5+lg5= .
考点:对数的运算性质
专题:函数的性质及应用
分析:利用对数的换底公式、lg2+lg5=1即可得出.
解答:
解:原式=
•
+lg2(lg2+lg5)+lg5
=2+lg2+lg5
=2+1
=3.
故答案为:3.
| lg3 |
| lg2 |
| 2lg2 |
| lg3 |
=2+lg2+lg5
=2+1
=3.
故答案为:3.
点评:本题考查了对数的换底公式、lg2+lg5=1,属于基础题.

练习册系列答案
相关题目
函数f(x)=2x-1,x∈{-1,1},则f(x)的值域为( )
| A、[-3,1) |
| B、(-3,1] |
| C、[-3,1] |
| D、{-3,1} |
已知函数f(x)=|x-1|,则下列函数与f(x)相等的函数是( )
A、g(x)=
| |||||||
B、g(x)=
| |||||||
C、g(x)=
| |||||||
| D、g(x)=x-1 |
设0<θ<
,
=(sin2θ,cosθ),
=(cosθ,1),若
∥
,则tanθ=( )
| π |
| 2 |
| a |
| b |
| a |
| b |
A、
| ||
| B、2 | ||
| C、1 | ||
| D、0 |
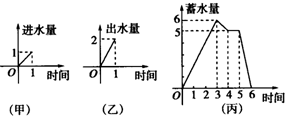 水池有两个相同的进水口和一个出水口,每个口进出水速度如下图(甲)、(乙)所示,某天0点到6点该水池蓄水量如图(丙)所以(至少打开一个水口)给出以下3个论断:
水池有两个相同的进水口和一个出水口,每个口进出水速度如下图(甲)、(乙)所示,某天0点到6点该水池蓄水量如图(丙)所以(至少打开一个水口)给出以下3个论断: