题目内容
3.数列{an}中,对任意自然数n∈N*,恒有a1+a2+…+an=2n-1,则a12+a22+a32…+an2=$\frac{1}{3}$(4n-1).分析 由题意易得an=2n-1,可得{an2}是1为首项,4为公比的等比数列,由等比数列的求和公式可得.
解答 解:当n=1时,可得a1=21-1=1,
当n≥2时,an=(a1+a2+…+an)-(a1+a2+…+an-1)
=(2n-1)-(2n-1-1)=2n-1,
当n=1时上式也适合,∴an=2n-1,
∴$\frac{{{a}_{n+1}}^{2}}{{{a}_{n}}^{2}}$=$\frac{{2}^{2n}}{{2}^{2n-2}}$=4,
∴{an2}是1为首项,4为公比的等比数列,
∴a12+a22+a32…+an2=$\frac{1×(1-{4}^{n})}{1-4}$=$\frac{1}{3}$(4n-1).
故答案为:$\frac{1}{3}$(4n-1).
点评 本题考查等比数列的求和公式,涉及等比数列的判定,考查运算能力,属基础题.

练习册系列答案
相关题目
13.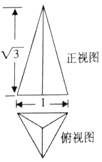 若正三棱锥的正视图与俯视图如图所示,则它的侧视图的面积为( )
若正三棱锥的正视图与俯视图如图所示,则它的侧视图的面积为( )
 若正三棱锥的正视图与俯视图如图所示,则它的侧视图的面积为( )
若正三棱锥的正视图与俯视图如图所示,则它的侧视图的面积为( )| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{4}$ |