题目内容
2.以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为$ρ=2({sinθ+cosθ+\frac{1}{ρ}})$.(1)求曲线C的参数方程;
(2)在曲线C上任取一点P(x,y),求的3x+4y最大值.
分析 (1)根据y=ρsinθ,x=ρcosθ,求出C的普通方程,从而求出参数方程即可;
(2)设出P的坐标,从而求出3x+4y的最大值即可.
解答 解:(1)由$ρ=2({sinθ+cosθ+\frac{1}{ρ}})$,得ρ2=2(ρsinθ+ρcosθ+1),
∴x2+y2=2x+2y+2,即(x-1)2+(y-1)2=4,
故曲线C的参数方程为$\left\{\begin{array}{l}x=1+2cosθ\\ y=1+2sinθ\end{array}\right.(θ$为参数).
(2)由(1)可设点P的坐标为(1+2cosθ,1+2sinθ),θ∈[0,2π),
∴3x+4y=3+6cosθ+4+8sinθ=7+10sin(θ+φ),
∴(3x+4y)max=7+10=17.
点评 本题考查了极坐标方程以及参数方程和普通方程的转化,考查求函数的最大值问题,是一道中档题.

练习册系列答案
相关题目
12.函数f(x)=x2-x-2(-5≤x≤5),在其定义域内任取一点x0,使f(x0)<0的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{4}{5}$ |
10.若a=60.3,b=log0.30.6,c=log6sin1,则a、b、c的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
17.在△ABC中,tanA=$\frac{1}{2}$,cosB=$\frac{3\sqrt{10}}{10}$,则tanC=( )
| A. | -2 | B. | 1 | C. | $\sqrt{3}$ | D. | -1 |
7.如图描述的是我国2014年四个季度与2015年前三个季度三大产业GDP累计同比贡献率,以下结论正确的是( )


| A. | 2015年前三个季度中国GDP累计比较2014年同期增速有上升的趋势 | |
| B. | 相对于2014年,2015年前三个季度第三产业对GDP的贡献率明显增加 | |
| C. | 相对于2014年,2015年前三个季度第二产业对GDP的贡献率明显增加 | |
| D. | 相对于2014年,2015年前三个季度第一产业对GDP的贡献率明显增加 |
20.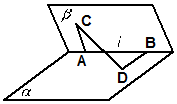 如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )
如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )
 如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )
如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )| A. | $\sqrt{11}$ | B. | $\sqrt{14}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{23}$ |
1.已知全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则(∁UM)∪(∁UN)=( )
| A. | {2,4} | B. | {2,3,5} | C. | {1,3,4,5} | D. | {2,3,4,5} |