Question

在半径为R的圆内，作内接等腰三角形，当底边上高为多少时，它的面积最大？

Answer 1

考点：球内接多面体,棱柱、棱锥、棱台的体积

专题：综合题,空间位置关系与距离

分析：设高为h，底为2x，得到a和h的关系，进而求得三角形面积的表达式，对面积的解析式求导，然后令S′=0，即可求得h．三角形面积最大．

解答： 解：如图，设圆内接等腰三角形的底边长为2x，高为h，那么
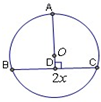h=AO+DO=R+

R2-x2

，
解得x²=h（2R-h），于是内接三角形的面积为：S=x•h=

h(2R-h)

•h=

(2Rh3-h4)

，
从而S′=

1

2

(2Rh3-h4)-

1

2

(2Rh3-h4)′=

1

2

(2Rh3-h4)-

1

2

(6Rh2-4h2)=

h2(3R-2h)

(2R-h)h3

，
令S′=0，解得h=

3

2

R，由于不考虑不存在的情况，所在区间（0，2R）上列表示如下：

h	(0， 3 2 R)	3 2 R	( 3 2 R，2R)
S′	+	0	-
S	增函数	最大值	减函数

由此表可知，当h=

3

2

R时，等腰三角形的面积最大

点评：本题主要考查了利用导数研究函数的极值．解题的关键是利用导函数求得函数取最值时，h的值．