题目内容
12.已知z=(m+4)+(m-2)i在复平面内对应的点在第三象限,则实数m的取值范围是( )| A. | (-4,2) | B. | (-2,4) | C. | (2,+∞) | D. | (-∞,-4) |
分析 z=(m+4)+(m-2)i在复平面内对应的点在第三象限,可得$\left\{\begin{array}{l}{m+4<0}\\{m-2<0}\end{array}\right.$,解出即可得出.
解答 解:z=(m+4)+(m-2)i在复平面内对应的点在第三象限,∴$\left\{\begin{array}{l}{m+4<0}\\{m-2<0}\end{array}\right.$,
解得:m<-4
则实数m的取值范围是(-∞,-4).
故:D.
点评 本题考查了复数的几何意义、不等式的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
2.命题“?x∈R,x2-x+1>0”的否定是( )
| A. | ?x∈R,x2-x+1≤0 | B. | ?x∈R,x2-x+1<0 | ||
| C. | ?x0∈R,x02-x0+1≤0 | D. | ?x0∈R,x02-x0+1<0 |
20.已知函数f(x)=cos(2x-φ)-$\sqrt{3}$sin(2x-φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后关于y轴对称,则f(x)在区间$[{-\frac{π}{2},0}]$上的最小值为( )
| A. | -1 | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | -2 |
4.若x>0,y>0,x+y=1,则$\frac{x^2}{x+2}+\frac{y^2}{y+1}$的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{2}$ |
2.集合A={x|x2-2x<0},B={x||x|<2},则( )
| A. | A∩B=∅ | B. | A∩B=A | C. | A∪B=A | D. | A∪B=R |
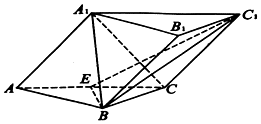 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.