题目内容
4.若x>0,y>0,x+y=1,则$\frac{x^2}{x+2}+\frac{y^2}{y+1}$的最小值为( )| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{2}$ |
分析 通过换元利用导数研究函数的单调性极值与最值即可得出.
解答 解:x>0,y>0,x+y=1,则y=1-x.
∴$\frac{x^2}{x+2}+\frac{y^2}{y+1}$=$\frac{{x}^{2}-4+4}{x+2}$+$\frac{(1-x)^{2}}{2-x}$=x-2+$\frac{4}{x+2}$+$\frac{(2-x)^{2}+2x-4+1}{2-x}$
=x-2+$\frac{4}{x+2}$+2-x-2+$\frac{1}{2-x}$=$\frac{4}{x+2}$-2+$\frac{1}{2-x}$=f(x),
f′(x)=$\frac{-4}{(x+2)^{2}}$+$\frac{1}{(2-x)^{2}}$=$\frac{(x+2)^{2}-4(x-2)^{2}}{(4-{x}^{2})^{2}}$=$\frac{-3(x-\frac{2}{3})(x-6)}{(4-{x}^{2})^{2}}$,0<x<1.
可知:当x=$\frac{2}{3}$,y=$\frac{1}{3}$时,f(x)取得最小值为:$\frac{4}{\frac{2}{3}+2}$-2+$\frac{1}{2-\frac{2}{3}}$=$\frac{1}{4}$.
故选:A.
点评 本题考查了换元方法、利用导数研究函数的单调性极值与最值、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.cos75°cos15°-sin255°sin165°的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 0 |
15.已知关于x的方程sinx+cosx=m在[0,π]有两个不等的实根,则m的一个值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
12.已知z=(m+4)+(m-2)i在复平面内对应的点在第三象限,则实数m的取值范围是( )
| A. | (-4,2) | B. | (-2,4) | C. | (2,+∞) | D. | (-∞,-4) |
16.设x、y满足不等式组$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y-10≤0}\\{y≤2}\end{array}\right.$,则z=x2+y2的最小值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
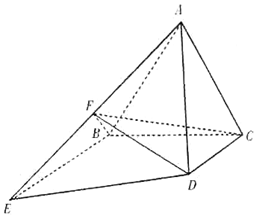 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.