题目内容
1.已知函数f(x)是定义在(0,+∞)上的单调函数,且对任意的正数x、y都有f(x•y)=f(x)+f(y),若数列{an}的前n项和为Sn,且f(an)=f(Sn+2)-f(4)(n∈N*),则数列{an}的通项公式an=$\frac{1}{2}$×($\frac{4}{3}$)n.分析 由f(an)=f(Sn+2)-f(4),即为(an)=f(Sn+2)-f(4),由条件可得f(Sn+2)=f(4an),由单调性可得Sn+2=4a.,求得首项,将n换为n-1,相减,运用等差数列的通项公式.
解答 解:∵对任意的正数x、y都有f(x•y)=f(x)+f(y),
且f(an)=f(Sn+2)-f(4)(n∈N*),
∴f(Sn+2)=f(an)+f(4)=f(4•an),
又∵函数f(x)是定义在(0,+∞)上的单调函数,
∴Sn+2=4an…①.
当n=1时,S1+2=a1+2=4a1,解得a1=$\frac{2}{3}$.
当n≥2时,Sn-1+2=4an-1…②.
①-②得:an=4an-4an-1,即$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{4}{3}$.
∴数列{an}是一个以$\frac{2}{3}$为首项,以$\frac{4}{3}$为公比的等比数列,
∴an=$\frac{2}{3}•(\frac{4}{3})^{n-1}$=$\frac{1}{2}$×($\frac{4}{3}$)n.
故答案为:$\frac{1}{2}$×($\frac{4}{3}$)n.
点评 本题考查函数的单调性的运用,抽象函数的运用,考查数列的通项的求法,注意运用通项和前n项和的关系,考查等差数列的通项公式的运用,属于中档题.

练习册系列答案
相关题目
12.已知z=(m+4)+(m-2)i在复平面内对应的点在第三象限,则实数m的取值范围是( )
| A. | (-4,2) | B. | (-2,4) | C. | (2,+∞) | D. | (-∞,-4) |
16.设x、y满足不等式组$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y-10≤0}\\{y≤2}\end{array}\right.$,则z=x2+y2的最小值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
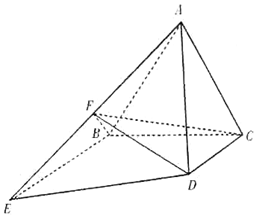 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.