题目内容
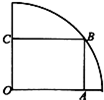 如图,在半径为3m的
如图,在半径为3m的| 1 |
| 4 |
(1)写出体积V关于x的函数关系式,并指出定义域;
(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?最大体积是多少?
考点:导数在最大值、最小值问题中的应用,函数解析式的求解及常用方法
专题:应用题,导数的综合应用
分析:(1)连接OB,在Rt△OAB中,由AB=x,利用勾股定理可得OA=
,设圆柱底面半径为r,则
=2πr,即可得出r.利用V=πr2•x(其中0<x<30)即可得出.
(2)利用导数V′,得出其单调性,即可得出结论.
| 9-x2 |
| 9-x2 |
(2)利用导数V′,得出其单调性,即可得出结论.
解答:
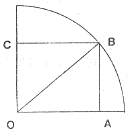 解:(1)连接OB,在Rt△OAB中,∵AB=x,∴OA=
解:(1)连接OB,在Rt△OAB中,∵AB=x,∴OA=
,
设圆柱底面半径为r,则
=2πr,
即4π2r2=9-x2,
∴V=πr2•x=
,其中0<x<3.…(6分)
(2)由V′=
=0及0<x<3,得x=
,…(8分)
列表如下:
…(10分)
所以当x=
时,V有极大值,也是最大值为
.…(14分)
答:当x为
m时,做出的圆柱形罐子体积最大,最大体积是
m3.…(16分)
 解:(1)连接OB,在Rt△OAB中,∵AB=x,∴OA=
解:(1)连接OB,在Rt△OAB中,∵AB=x,∴OA=| 9-x2 |
设圆柱底面半径为r,则
| 9-x2 |
即4π2r2=9-x2,
∴V=πr2•x=
| 9x-x3 |
| 4π |
(2)由V′=
| 9-3x2 |
| 4π |
| 3 |
列表如下:
| x | (0,
|
| (
| ||||||
| V′ | + | 0 | - | ||||||
| V | 极大值
|
所以当x=
| 3 |
3
| ||
| 2π |
答:当x为
| 3 |
3
| ||
| 2π |
点评:熟练掌握勾股定理、圆柱的体积计算公式、利用导数研究函数的单调性极值与最值等是解题的关键.

练习册系列答案
相关题目
已知函数f(x)=5x-3sinx,x∈(-2,2),如果f(1-a)+f(1-a2)<0成立,则实数a的取值范围为( )
A、(1,
| ||
| B、(1,3) | ||
| C、(-∞,-2)∪(1,+∞) | ||
| D、(-2,1) |
数列{(-1)n•n}的前2015项的和S2015为( )
| A、-2013 | B、-1008 |
| C、2013 | D、1008 |
设定点F1(-3,0),F2(3,0),动点P(x,y)满足条件|PF1|+|PF2|=6,则动点P的轨迹是( )
| A、椭圆 | B、线段 |
| C、双曲线 | D、椭圆或线段 |
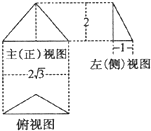 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的四个表面中,面积的最大值为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的四个表面中,面积的最大值为