题目内容
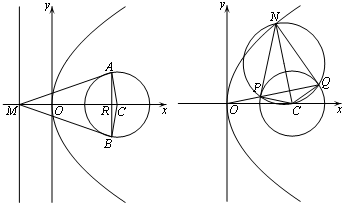
已知抛物线E:y2=2px(p>0)的准线与x轴交于点M,过点M作圆C:(x-2)2+y2=1的两条切线,切点为A,B,|AB|=
.
(Ⅰ)求抛物线E的方程;
(Ⅱ)过抛物线E上的点N作圆C的两条切线,切点分别为P,Q,若P,Q,O(O为原点)三点共线,求点N的坐标.
4
| ||
| 3 |
(Ⅰ)求抛物线E的方程;
(Ⅱ)过抛物线E上的点N作圆C的两条切线,切点分别为P,Q,若P,Q,O(O为原点)三点共线,求点N的坐标.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设AB与x轴交于点R,求出|AR|,|CR|,即可求抛物线E的方程;
(Ⅱ)求出圆D,C的方程,两圆相减,可得直线PQ的方程,利用直线PQ经过点O,即可求点N的坐标.
(Ⅱ)求出圆D,C的方程,两圆相减,可得直线PQ的方程,利用直线PQ经过点O,即可求点N的坐标.
解答:
 解:(Ⅰ)由已知得M(-
解:(Ⅰ)由已知得M(-
,0),C(2,0).
设AB与x轴交于点R,
由圆的对称性可知,|AR|=
.
于是|CR|=
=
,
所以|CM|=
=
=3,
即2+
=3,p=2.
故抛物线E的方程为y2=4x.…(5分)
(Ⅱ)设N(s,t).
P,Q是NC为直径的圆D与圆C的两交点.
圆D方程为(x-
)2+(y-
)2=
,
即x2+y2-(s+2)x-ty+2s=0.①
又圆C方程为x2+y2-4x+3=0.②
②-①得(s-2)x+ty+3-2s=0.③…(9分)
P,Q两点坐标是方程①和②的解,也是方程③的解,从而③为直线PQ的方程.
因为直线PQ经过点O,所以3-2s=0,s=
.
故点N坐标为(
,
)或(
,-
).…(12分)
 解:(Ⅰ)由已知得M(-
解:(Ⅰ)由已知得M(-| p |
| 2 |
设AB与x轴交于点R,
由圆的对称性可知,|AR|=
2
| ||
| 3 |
于是|CR|=
| |AC|2+|AR|2 |
| 1 |
| 3 |
所以|CM|=
| |AC| |
| sin∠AMC |
| |AC| |
| sin∠CAR |
即2+
| p |
| 2 |
故抛物线E的方程为y2=4x.…(5分)
(Ⅱ)设N(s,t).
P,Q是NC为直径的圆D与圆C的两交点.
圆D方程为(x-
| s+2 |
| 2 |
| t |
| 2 |
| (s-2)2+t2 |
| 4 |
即x2+y2-(s+2)x-ty+2s=0.①
又圆C方程为x2+y2-4x+3=0.②
②-①得(s-2)x+ty+3-2s=0.③…(9分)
P,Q两点坐标是方程①和②的解,也是方程③的解,从而③为直线PQ的方程.
因为直线PQ经过点O,所以3-2s=0,s=
| 3 |
| 2 |
故点N坐标为(
| 3 |
| 2 |
| 6 |
| 3 |
| 2 |
| 6 |
点评:本题考查抛物线的方程,考查圆的方程,考查两圆的位置关系,考查学生分析解决问题的能力,求得PQ的方程是关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
平面内点P(x,y)的坐标满足方程
=
,则动点P的轨迹是( )
| (x-1)2+(y-1)2 |
| |x+y-2| | ||
|
| A、椭圆 | B、双曲线 |
| C、抛物线 | D、直线 |
命题P:自然数a,b,c中恰有一个偶数,则其否定?P为( )
| A、a,b,c都是奇数 |
| B、a,b,c都是偶数 |
| C、a,b,c中至少有两个偶数 |
| D、a,b,c中至少有两个偶数或都是奇数 |
已知a=log20.3,b=20.3,c=0.20.3,则a,b,c三者的大小关系是( )
| A、b>c>a |
| B、b>a>c |
| C、a>b>c |
| D、c>b>a |