题目内容
已知x∈R,a>0,设ax+a-x=u,将下列各式分别用u表示
(1)a
+a-
;
(2)a
+a-
.
(1)a
| x |
| 2 |
| x |
| 2 |
(2)a
| 3x |
| 2 |
| 3x |
| 2 |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:(1)利用“完全平方公式”即可得出;
(2)利用“立方和公式”即可得出.
(2)利用“立方和公式”即可得出.
解答:
解:(1)∵(a
+a-
)2=ax+a-x2+2=u+2,a>0,
∴a
+a-
=
.
(2)a
+a-
=(a
+a-
)(ax+a-x-1)=
(u-1).
| x |
| 2 |
| x |
| 2 |
∴a
| x |
| 2 |
| x |
| 2 |
| u+2 |
(2)a
| 3x |
| 2 |
| 3x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| u+2 |
点评:本题考查了乘法公式、指数幂的运算法则,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
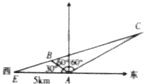 如图,某海岛观察哨A测得在海岛北偏东60°的C处有一轮船,80分钟后测得船在海岛北偏西60°的B处,又过20分钟轮船到达位于海岛正西方且距离海岛5km的E港口,如果轮船始终作匀速直线运动,问船速多少?
如图,某海岛观察哨A测得在海岛北偏东60°的C处有一轮船,80分钟后测得船在海岛北偏西60°的B处,又过20分钟轮船到达位于海岛正西方且距离海岛5km的E港口,如果轮船始终作匀速直线运动,问船速多少?已知函数f(x)=-x2+x,则f(x)从-1到-0.9的平均变化率为( )
| A、3 | B、0.29 |
| C、2.09 | D、2.9 |
将cos(π+2)化为某个锐角的三角函数为( )
| A、cos2 |
| B、-cos2 |
| C、-cos(π-2) |
| D、cos(π-2) |
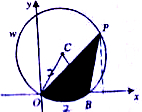 如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴正半轴于点B(2,0),P是弧OwB上的一个动点,且∠OPB=30°,设P点坐标为(m,n).
如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴正半轴于点B(2,0),P是弧OwB上的一个动点,且∠OPB=30°,设P点坐标为(m,n).