题目内容
15.已知圆C:x2+(y-4)2=4,直线l过点(-2,0).(1)当直线l与圆C相切时,求直线l的一般式方程;
(2)当直线l与圆C相交于A、B两点,且|AB|≥2$\sqrt{2}$时,求直线l斜率的取值范围.
分析 (1)当直线l的斜率不存在时,直线l的方程为x=-2;当直线l的斜率k存在时,设直线l的方程为y=k(x+2),由圆心C(0,4)到直线l的距离等于半径,能求出直线l的方程.
(2)圆C:x2+(y-4)2=4的圆心C(0,4),半径r=2,设直线l的方程为y=k(x+2),由直线l与圆C相交于A、B两点,且|AB|≥2$\sqrt{2}$,列出不等式,由此能求出直线l斜率的取值范围.
解答 解:(1)当直线l的斜率不存在时,直线l的方程为x=-2,满足条件;
当直线l的斜率k存在时,设直线l的方程为y=k(x+2),
则圆心C(0,4)到直线l的距离:
d=$\frac{|0-4+2k|}{\sqrt{1+{k}^{2}}}$=2,解得k=$\frac{3}{4}$,
∴直线l的方程为:y=$\frac{3}{4}$(x+2),
综上,直线l的方程为3x-4y+6=0或x=-2.
(2)圆C:x2+(y-4)2=4的圆心C(0,4),半径r=2,
设直线l的方程为y=k(x+2),
直线l与圆C相交于A、B两点,且|AB|≥2$\sqrt{2}$,
则圆心C(0,4)到直线l的距离:
d=$\frac{|2k-4|}{\sqrt{1+{k}^{2}}}$≤$\sqrt{{r}^{2}-(\frac{|AB|}{2})^{2}}$=$\sqrt{4-2}$=$\sqrt{2}$,
解得1≤k≤7,
∴直线l斜率的取值范围是[1,7].
点评 本题考查切线方程的求法,考查直线斜率的取值范围的求法,考查圆的性质、直线与圆的位置关系,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
5.若实数x,y满足x2+y2+4x-2y+4=0,则$\frac{y}{x}$的取值范围是( )
| A. | $({-∞,-\frac{4}{3}}]∪[{0,+∞})$ | B. | $({-∞,-\frac{3}{4}}]∪[{0,+∞})$ | C. | $[{-\frac{3}{4},0}]$ | D. | $[{-\frac{4}{3},0}]$ |
3.以椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的中心为原点,左焦点为焦点的抛物线的标准方程是( )
| A. | x2=8y | B. | y2=16x | C. | x2=-8y | D. | y2=-16x |
4.求值:tan210°=( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
5.已知f(x)为定义在(0,+∞)上的可导函数,且f(x)>xf'(x),则不等式${x^2}f(\frac{1}{x})-f(x)<0$的解集为( )
| A. | (0,4) | B. | (0,3) | C. | (0,2) | D. | (0,1) |
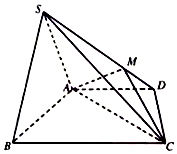 如图,在四棱锥S-ABCD中,底面梯形ABCD中,AD∥BC,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2CD=2\sqrt{5}$,M是SD上任意一点,$\overrightarrow{SM}=m\overrightarrow{MD}$,且m>0.
如图,在四棱锥S-ABCD中,底面梯形ABCD中,AD∥BC,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2CD=2\sqrt{5}$,M是SD上任意一点,$\overrightarrow{SM}=m\overrightarrow{MD}$,且m>0.