题目内容
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与道路垂直,且∠ABC=120°,路灯C采用锥形灯罩,射出的光线如图中阴影部分所示,已知∠ACD=60°,路宽AD=24 m,设灯柱高AB=h(m),∠ACB=θ(30°≤θ≤45°).
(1) 求灯柱的高h(用θ表示);
(2) 若灯杆BC与灯柱AB所用材料相同,记此用料长度和为S,求S关于θ的函数解析式,并求出S的最小值.
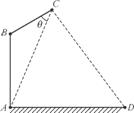
(第11题)

(第11题)
(1) 因为∠ABC=120°,∠ACB=θ,
所以∠BAC=60°-θ,因为∠BAD=90°,
所以∠CAD=30°+θ,
因为∠ACD=60°,
所以∠ADC=90°-θ.
在△ACD中,
因为 =
= ,
,
所以AC= =16
=16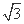 cos θ.
cos θ.
在△ABC中,因为 =
= ,
,
所以AB= =16sin2θ,即h=16sin2θ.
=16sin2θ,即h=16sin2θ.
(2) 在△ABC中,因为 =
= ,
,
所以BC= =32cos θsin(60°-θ)=8
=32cos θsin(60°-θ)=8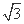 +8
+8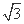 cos 2θ-8sin 2θ,
cos 2θ-8sin 2θ,
则S=AB+BC=8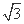 +8
+8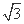 cos 2θ+8sin 2θ=8
cos 2θ+8sin 2θ=8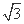 +16sin(2θ+60°).
+16sin(2θ+60°).
因为30°≤θ≤45°,所以120°≤2θ+60°≤150°.
所以当θ=45°时,S取得最小值为(8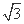 +8) m.
+8) m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.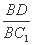 的值.
的值.
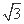 sinxcosx在区间
sinxcosx在区间 上的最大值是 .
上的最大值是 . 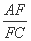 的值.
的值.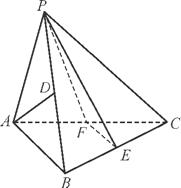
 中,a1=1,a2=2,且an+2=an+1+(-1)n(n∈N*),则S100= .
中,a1=1,a2=2,且an+2=an+1+(-1)n(n∈N*),则S100= . 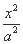 +
+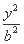 =1的焦点在x轴上,过点
=1的焦点在x轴上,过点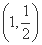 作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆的方程是 .
作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆的方程是 .