题目内容
己知抛物线y2=2px(p>0)的准线恰好过双曲线
-
=1(a>0,b>0)的左焦点,两条曲线的交点的连线过双曲线的右焦点,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先根据抛物线方程得到焦点坐标和交点坐标,代入双曲线,把
=c代入整理得 c4-6a2c2+a4=0等式两边同除以a4,得到关于离心率e的方程,进而可求得e.
| p |
| 2 |
解答:
解:由题意,∵两条曲线交点的连线过点F
∴两条曲线交点为(
,p),
代入双曲线方程得
-
=1,
又
=c
代入化简得 c4-6a2c2+a4=0
∴e4-6e2+1=0
∴e2=3+2
=(1+
)2
∴e=
+1
故选:A.
∴两条曲线交点为(
| p |
| 2 |
代入双曲线方程得
| ||
| a2 |
| p2 |
| b2 |
又
| p |
| 2 |
代入化简得 c4-6a2c2+a4=0
∴e4-6e2+1=0
∴e2=3+2
| 2 |
| 2 |
∴e=
| 2 |
故选:A.
点评:本题考查由圆锥曲线的方程求焦点、考查双曲线的三参数的关系:c2=a2+b2注意与椭圆的区别.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
若双曲线C:4x2-y2=λ(λ>0)与抛物线y2=4x的准线交于A,B两点,且|AB|=2
,则λ的值是( )
| 3 |
| A、1 | B、2 | C、4 | D、13 |
下列命题中错误的是( )
| A、命题“若x2-5x+6=0,则x=3”的逆否命题是“若x≠3,则x2-5x+6≠0” | ||
| B、已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假 | ||
C、若x、y∈R,则“x=y”是xy≥(
| ||
| D、对命题p:?x∈R,使x2+x+2<0,则¬p:?x∈R,则x2+x+2≥0 |
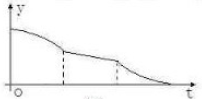
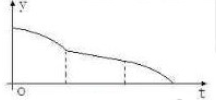
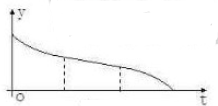
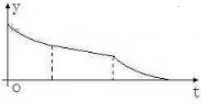
 已知某几何体的三视图如图所示,其中正视图与侧视图都是直角边为2的等腰直角三角形,则该几何体的表面积为
已知某几何体的三视图如图所示,其中正视图与侧视图都是直角边为2的等腰直角三角形,则该几何体的表面积为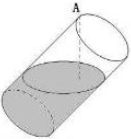 一空的圆柱体容器直径小于母线长斜放,将容器斜放,使圆柱的母线与水平面成45°角,现于这种状态下由容器的最高点A处匀速地灌油,如图,则点A到油平面的距离y与灌水时间t的函数图象大致为( )
一空的圆柱体容器直径小于母线长斜放,将容器斜放,使圆柱的母线与水平面成45°角,现于这种状态下由容器的最高点A处匀速地灌油,如图,则点A到油平面的距离y与灌水时间t的函数图象大致为( )