题目内容
已知角α的终边过点(3a-9,a+2)且cosα≤0,sinα>0,求实数a的取值范围.
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:由题意可得
,从而可求得实数a的取值范围.
|
解答:
解:∵cosα≤0且sinα>0,
∴
≤0且
>0.
∴
∴-2<a≤3.
∴实数m的取值范围为:-2<a≤3.
∴
| 3a-9 |
| r |
| a+2 |
| r |
∴
|
∴实数m的取值范围为:-2<a≤3.
点评:本题考查任意角的三角函数的定义及由三角函数值的符号确定参数范围,掌握任意角的三角函数的定义是关键,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a>0,设p:存在a∈R,使y=ax是R上的单调递减函数; q:存在a∈R,使函数g(x)=lg(2ax2+2x+1)的值域为R,如果“p∧q”为假,“p∨q”为真,则a的取值范围是( )
A、(
| ||
B、(
| ||
C、(0,
| ||
D、(0,
|
直线l1:x+y-2
=0与直线l2:
(t为参数)的交点到原点O的距离是( )
| 2 |
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
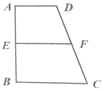 如图梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论:
如图梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论: