题目内容
1.已知数列{an}中,a1=2,an+1=an+$\frac{1}{3}$(n∈N*),则该数列的通项公式为:an=$\frac{n+5}{3}$.分析 根据题意,由an+1=an+$\frac{1}{3}$分析可得数列{an}为等差数列,进而可得首项a1=2,公差d=$\frac{1}{3}$,由等差数列的通项公式计算可得答案.
解答 解:根据题意,数列{an}中,an+1=an+$\frac{1}{3}$(n∈N*),
则有an+1-an=$\frac{1}{3}$(n∈N*),
即数列{an}为等差数列,其首项a1=2,公差d=$\frac{1}{3}$,
则其通项an=a1+(n-1)d=$\frac{n+5}{3}$,
故答案为:an=$\frac{n+5}{3}$.
点评 本题考查等差数列的通项公式,关键是分析出数列{an}为等差数列.

练习册系列答案
相关题目
16.已知单调函数f(x)满足f(0)=3,且f(f(x)-ex-x)=e2+4,则函数零点所在区间为( )
| A. | (-4,-3) | B. | (-3,-2) | C. | (-2,-1) | D. | (-1,0) |
13.一个锥体的正视图和俯视图如图所示,则该锥体外接球的半径是( )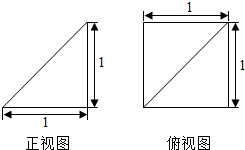

| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |