题目内容
已知点P(x,y,z)的坐标满足x2+y2+z2=4,且点A的坐标为(2,3,2
),则|PA|的最小值为( )
| 3 |
| A、5 | B、2 | C、3 | D、4 |
考点:空间两点间的距离公式
专题:计算题,空间位置关系与距离
分析:由题意,|PA|的最小值为A到球心的距离减去半径,即可得出结论.
解答:
解:由题意,|PA|的最小值为A到球心的距离减去半径,
∴|PA|的最小值为
-2=3,
故选:C.
∴|PA|的最小值为
22+32+(2
|
故选:C.
点评:本题考查空间距离的计算,考查学生分析解决问题的能力,正确转化是关键.

练习册系列答案
相关题目
直线
x+y-b=0截圆x2+y2-4y=0所得的劣弧所对的圆心角为
,则实数b的值是( )
| 3 |
| 2π |
| 3 |
A、2+2
| ||
| B、4 | ||
C、2±2
| ||
| D、0或4 |
若复数z的共轭复数为
,且满足
(2-i)=10+5i(i为虚数单位),则|z|=( )
. |
| z |
. |
| z |
| A、25 | ||
| B、10 | ||
| C、5 | ||
D、
|
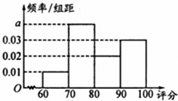 为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.
为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.