题目内容
下列三个命题：
①若
+
+
=
，则A1，A2，A3三点共面；
②若
+
+
+
=
，则A1，A2，A3，A4四点共面；
③若
+
+
+…+
+
=
，则A1，A2，A3，…，An这n个点共面．
其中是真命题的为（ ）
①若
| A1A2 |
| A2A3 |
| A3A1 |
| 0 |
②若
| A1A2 |
| A2A3 |
| A3A4 |
| A4A1 |
| 0 |
③若
| A1A2 |
| A2A3 |
| A3A4 |
| An-1An |
| AnA1 |
| 0 |
其中是真命题的为（ ）
| A、① | B、② | C、①② | D、①②③ |
考点：空间向量的加减法
专题：空间向量及应用
分析：①根据
+
+
=
，得出A1，A2，A3三点共面；
②当
+
+
+
=
时，A1，A2，A3，A4四点不一定共面；
③当
+
+
+…+
+
=
时，这n个点不一定共面．
| A1A2 |
| A2A3 |
| A3A1 |
| 0 |
②当
| A1A2 |
| A2A3 |
| A3A4 |
| A4A1 |
| 0 |
③当
| A1A2 |
| A2A3 |
| A3A4 |
| An-1An |
| AnA1 |
| 0 |
解答：
解：①∵
+
+
=
，
∴向量
、
、
在一条直线上或组成三角形，
∴A1，A2，A3三点共面，①正确；
②当
+
+
+
=
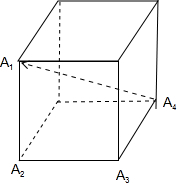
时，如图所示，
A1，A2，A3，A4四点不共面，∴②错误；
③当
+
+
+…+
+
=
时，
A1，A2，A3，…，An这n个点不一定共面，③错误．
综上，正确的命题是①．
故选：A．
解：①∵| A1A2 |
| A2A3 |
| A3A1 |
| 0 |
∴向量
| A1A2 |
| A2A3 |
| A3A1 |
∴A1，A2，A3三点共面，①正确；
②当
| A1A2 |
| A2A3 |
| A3A4 |
| A4A1 |
| 0 |
A1，A2，A3，A4四点不共面，∴②错误；
③当
| A1A2 |
| A2A3 |
| A3A4 |
| An-1An |
| AnA1 |
| 0 |
A1，A2，A3，…，An这n个点不一定共面，③错误．
综上，正确的命题是①．
故选：A．
点评：本题考查了空间向量的应用问题，解题时应根据空间向量的几何意义，应用举例的方法，是基础题目．
练习册系列答案
相关题目
已知函数y=f（x）为定义在R上的奇函数，且x＞0时，f（x）=lg（x2-ax+10），若函数y=f（x）的值域为R，则实数a的取值范围是（ ）
A、（-∞，-2
| ||||
B、（-2
| ||||
C、（-2
| ||||
D、[6，2
|
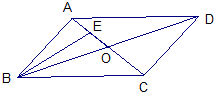如图，在平面四边形ABCD中，AC，BD相交于点O，E为线段AO的中点，若