题目内容
10．写出直线的斜截式方程：斜率是$\frac{2}{3}$，在y轴上的截距是10．分析 已知直线l的斜率为k，在y轴上的截距是b，则直线l的斜截式方程为y=kx+b．
解答 解：∵所求直线的斜率为$\frac{2}{3}$，又直线在y轴上的截距为10，
由直线方程的斜截式得：y=$\frac{2}{3}$x+10，
化为一般式得：2x-3y+30=0．
点评 本题考查了直线的斜截式方程．考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
18．已知圆C的标准方程是（x-2）2+（y-4）2=k（k＞0），若圆C与y轴交于A，B两点，且点A在点B的上方，圆C与x轴交于E，F两点，且点E在点F的右方，则AE中点M的轨迹方程是（ ）
| A． | （y-2）2-（x-1）2=3（x＞1，y＞2+$\sqrt{3}$） | B． | （y-2）2-（x-1）2=3 | ||
| C． | （x-2）2-（y-1）2=3（y＞1，x＞2+$\sqrt{3}$） | D． | （x-2）2-（y-1）2=3 |
5．函数f（x）=$\frac{{2}^{x}-1}{{2}^{x}-10}$与数列{an}的通项公式an=$\frac{{2}^{n}-1}{{2}^{n}-10}$，则下列说法正确的是（ ）
| A． | 函数f（x）有最大值，数列{an}有最大项 | B． | 函数f（x）有最大值，数列{an}无最大项 | ||
| C． | 函数f（x）无最大值，数列{an}有最大项 | D． | 函数f（x）无最大值，数列{an}无最大项 |
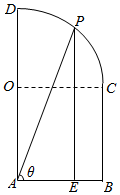已知$\widehat{CD}$是以O为圆心，以1为半径的四分之一圆，四边形OABC为正方形，P为$\widehat{CD}$上一动点，PE⊥AB于E．