题目内容
11．已知圆中一段弧的长正好等于该圆的外切正三角形的边长，那么这段弧所对的圆心角的弧度数为$2\sqrt{3}$．分析 如图所示，设△ABC的内切圆的半径r=1．在△BOD中，$\frac{BC}{2}$=BD=$\frac{OD}{tan30°}$，即可得出．
解答 解：如图所示，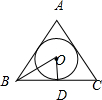
设△ABC的内切圆与边BC相切于点D，其圆心为O点，半径r=1．
连接OB，则OB平分∠ABC，∴∠OBD=30°．
在△BOD中，$\frac{BC}{2}$=BD=$\frac{OD}{tan30°}$=$\frac{1}{\frac{\sqrt{3}}{3}}$，
解得BC=2$\sqrt{3}$．
∵圆中一段弧长正好等于该圆的外切正三角形的边长，
∴这段弧所对的圆心角的弧度数为2$\sqrt{3}$．
故答案为：$2\sqrt{3}$．
点评 本题考查了三角形的内切圆的性质、正三角形的性质、含30°角的直角三角形的边角关系，属于基础题．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
4．$\int_1^e{（x+\frac{1}{x}}）dx$=（ ）
| A． | e2 | B． | $\frac{{{e^2}+1}}{2}$ | C． | $\frac{{{e^2}-1}}{2}$ | D． | $\frac{{{e^2}+3}}{2}$ |
5．已知P={x|-4≤x≤2，x∈Z}，Q={x|-3＜x＜1}，则P∩Q=（ ）
| A． | （-1，3） | B． | [-2，1） | C． | {0，1，2} | D． | {-2，-1，0} |
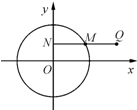如图，已知点M在圆O：x2+y2=4上运动，MN⊥y轴（垂足为N），点Q在NM的延长线上，且|QN|=2|MN|．