题目内容
17.若f(x)=-x2+ax+2+lg(2-|x|)(a∈R)是偶函数,且f(1-m)<f(m),则实数m的取值范围是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,2) | D. | (-1,$\frac{1}{2}$) |
分析 利用f(x)=-x2+ax+2+lg(2-|x|)(a∈R)是偶函数,求出a,确定定义域为(-2,2),在(0,2)上单调递减,f(1一m)<f(m),化为2>|1一m|>|m|,即可求出实数m的取值范围.
解答 解:∵f(x)=-x2+ax+2+lg(2-|x|)(a∈R)是偶函数,
∴f(-x)=f(x)即-x2-ax+2+lg(2-|x|)=-x2+ax+2+lg(2-|x|),
∴a=0,
∴f(x)=-x2+2+lg(2-|x|)定义域为(-2,2),在(0,2)上单调递减,
∵函数是偶函数,且f(1-m)<f(m),
∴f(|1-m|)<f(|m|),
∴2>|1-m|>|m|,
∴-1<m<$\frac{1}{2}$,
故选:D.
点评 本题考查函数的奇偶性、单调性,考查学生的计算能力,正确转化是关键,属于中档题.

练习册系列答案
相关题目
8.如果loga2>logb2>0,那么( )
| A. | 1<a<b | B. | 1<b<a | C. | 0<a<b<1 | D. | 0<b<a<1 |
5.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[0,1]上单调递增,设a=f(3),b=f($\sqrt{2}$),c=f(2),则a,b,c大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
12.已知|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=5,$\overrightarrow{a}$与$\overrightarrow{b}$不共线,若向量k$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直,则实数k的值为( )
| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | ±$\frac{3}{5}$ | D. | ±$\frac{5}{3}$ |
9.已知x∈R,符号[x]表示不超过x的最大整数,若函数f(x)=$\frac{[x]}{x}$(x>0),则给出以下四个结论正确的是( )
| A. | 函数f(x)的值域为[0,1] | |
| B. | 函数f(x)的图象是一条曲线 | |
| C. | 函数f(x)是(0,+∞)上的减函数 | |
| D. | 函数g(x)=f(x)-a有且仅有3个零点时$\frac{3}{4}$<a≤$\frac{4}{5}$ |
5.执行下面框图,则输出m的结果是( )


| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
6.函数y=$\frac{lg(x+1)}{x-2}$的定义域是( )
| A. | (-1,+∞) | B. | [-1,+∞) | C. | (-1,2)∪(2,+∞) | D. | [-1,2)∩(2,+∞) |
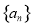 满足:①
满足:①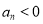 ;②
;②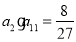 ;③
;③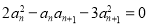 .
.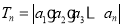 ,问:是否存在常数
,问:是否存在常数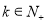 ,使得
,使得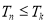 对于任意
对于任意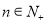 恒成立?若存在,请求出
恒成立?若存在,请求出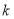 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.