题目内容
17．某几何体的三视图如图所示，则该几何体的表面积为（ ）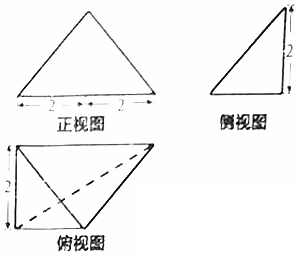
| A． | $6+4\sqrt{2}+2\sqrt{6}$ | B． | $4+6\sqrt{2}+2\sqrt{5}$ | C． | $4+2\sqrt{5}+2\sqrt{6}$ | D． | $4+6\sqrt{2}+2\sqrt{6}$ |
分析 由图形补全法，将图形补全为长方体，进而获得该几何体的直观图，得到几何体的表面积．
解答 解：由图形补全法，将图形补全为长方体，进而获得该几何体的直观图P-ABC，
再求得该几何体的表面积为：$S=\frac{1}{2}×2×2\sqrt{2}+\frac{1}{2}×2×4+\frac{1}{2}×2\sqrt{2}×2\sqrt{3}+\frac{1}{2}×4×2\sqrt{2}=4+6\sqrt{2}+2\sqrt{6}$．
故选D．
点评 本题考查了由几何体的三视图求几何体的表面积；关键是正确还原几何体．
练习册系列答案
阅读快车系列答案
相关题目
11．定义在R上的奇函数f（x）满足f（x-2）=f（x+2），且当x∈[-2，0]时，f（x）=3x-1，则f（9）=（ ）
| A． | -2 | B． | 2 | C． | $-\frac{2}{3}$ | D． | $\frac{2}{3}$ |
8．函数$y=sin（x+\frac{π}{4}）$在闭区间（ ）上为增函数．
| A． | $[-\frac{3}{4}π，\frac{π}{4}]$ | B． | [-π，0] | C． | $[-\frac{π}{4}，\frac{3}{4}π]$ | D． | $[-\frac{π}{2}，\frac{π}{2}]$ |
5．设随机变量X的分布列为P（X=k）=$\frac{k}{25}$，k=1，2，3，4，5，则P（$\frac{1}{2}$＜X＜$\frac{5}{2}$）等于（ ）
| A． | $\frac{2}{15}$ | B． | $\frac{2}{5}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{15}$ |
12．一个几何体的三视图如图所示，则这个几何体的（ ）
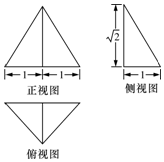
| A． | 外接球的体积为12$\sqrt{3}$ π | B． | 外接球的表面积为4π | ||
| C． | 体积为$\sqrt{2}$ | D． | 表面积为$\sqrt{5}$+$\sqrt{2}$+1 |
2．
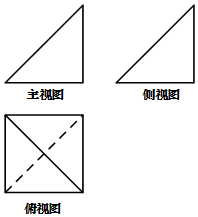某空间几何体的三视图如图所示，图中主视图和侧视图是两个全等的等腰直角三角形，腰长为4，俯视图中的四边形为正方形，则这个几何体的体积是（ ）
某空间几何体的三视图如图所示，图中主视图和侧视图是两个全等的等腰直角三角形，腰长为4，俯视图中的四边形为正方形，则这个几何体的体积是（ ）| A． | $\frac{32}{3}$ | B． | $\frac{64}{3}$ | C． | 16 | D． | 32 |
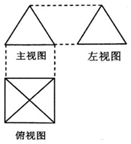如图，一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形，其俯视图轮廓为正方形，则其体积是$\frac{4\sqrt{3}}{3}$，表面积为12．