题目内容
已知幂函数f(x)的图象过点A(
,4),则幂函数的解析式f(x)= .
| 1 |
| 2 |
考点:幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:设出幂函数f(x)的解析式,由图象过点A,求出f(x)的解析式.
解答:
解:设幂函数f(x)=xa,
它的图象过点A(
,4),
∴(
)a=4,
解得a=-2;
∴f(x)=x-2.
故答案为:x-2.
它的图象过点A(
| 1 |
| 2 |
∴(
| 1 |
| 2 |
解得a=-2;
∴f(x)=x-2.
故答案为:x-2.
点评:本题考查了利用函数图象上的点求函数解析式的应用问题,是基础题目.

练习册系列答案
相关题目
平行于直线x+y-1=0且与圆x2+y2-2=0相切的直线的方程是( )
| A、x+y+2=0 | ||||
| B、x+y-2=0 | ||||
C、x+y+2
| ||||
| D、x+y+2=0或x+y-2=0 |
把二进制数110011(2)化为十进制数( )
| A、48 | B、49 | C、50 | D、51 |
已知M={x|(x+2)(x-1)>0},N={x|log2x<1},则M∩N=( )
| A、{x|-2<x<2} |
| B、{x|0<x<1} |
| C、{x|x<-2或x>1} |
| D、{x|1<x<2} |
下列正确的是( )
A、
| ||||||
B、
| ||||||
C、(
| ||||||
D、
|
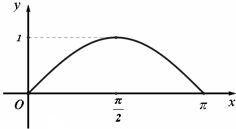
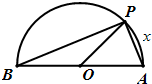 如图,点P在半径为1的半圆上运动,AB是直径,当P沿半圆弧从A到B运动时,点P经过的路程x与△APB的面积y的函数y=f(x)的图象是下图中的( )
如图,点P在半径为1的半圆上运动,AB是直径,当P沿半圆弧从A到B运动时,点P经过的路程x与△APB的面积y的函数y=f(x)的图象是下图中的( )