题目内容
已知数列 的各项均为正数,记
的各项均为正数,记 ,
, ,
,
 .
.
(Ⅰ)若 ,且对任意
,且对任意 ,三个数
,三个数 组成等差数列,求数列
组成等差数列,求数列 的通项公式.
的通项公式.
(Ⅱ)证明:数列 是公比为
是公比为 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意 ,三个数
,三个数 组成公比为
组成公比为 的等比数列.
的等比数列.
(Ⅰ) 因为对任意 ,三个数
,三个数 是等差数列,
是等差数列,
所以 . ………1分
. ………1分
所以 , ………2分
, ………2分
即 . ………3分
. ………3分
所以数列 是首项为1,公差为4的等差数列. ………4分
是首项为1,公差为4的等差数列. ………4分
所以 . ………5分
. ………5分
(Ⅱ)(1)充分性:若对于任意 ,三个数
,三个数 组成公比为
组成公比为 的等比数列,则
的等比数列,则
 . ………6分
. ………6分
所以 得
得
即 . ………7分
. ………7分
因为当 时,由
时,由 可得
可得 , ………8分
, ………8分
所以 .
.
因为 ,
,
所以 .
.
即数列 是首项为
是首项为 ,公比为
,公比为 的等比数列, ………9分
的等比数列, ………9分
(2)必要性:若数列 是公比为
是公比为 的等比数列,则对任意
的等比数列,则对任意 ,有
,有
 . ………10分
. ………10分
因为 ,
,
所以 均大于
均大于 .于是
.于是
 ………11分
………11分
 ………12分
………12分
即 =
= =
= ,所以三个数
,所以三个数 组成公比为
组成公比为 的等比数列.
的等比数列.
………13分
综上所述,数列 是公比为
是公比为 的等比数列的充分必要条件是:对任意n∈N﹡,三个数
的等比数列的充分必要条件是:对任意n∈N﹡,三个数 组成公比为
组成公比为 的等比数列. ………14分
的等比数列. ………14分

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 ,则tan α=________.
,则tan α=________. ;②
;②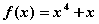 ;③
;③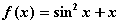 ; ④
; ④ 中 ,仅通过平移变换就能使函数图像为奇函数或偶函数图像的函数为( )
中 ,仅通过平移变换就能使函数图像为奇函数或偶函数图像的函数为( ) 的两个焦点,P为椭圆上一点且
的两个焦点,P为椭圆上一点且 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )



 则 “
则 “ ”是“
”是“ ”的( )
”的( )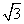 )x+
)x+ 上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )
上移动,经过点P的切线的倾斜角为α,则角α的取值范围是( )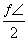 ) B.[0,
) B.[0,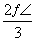 ,π) C.[
,π) C.[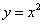 、
、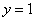 围成的区域的面积为
围成的区域的面积为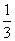 ; ② “
; ② “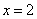 ”是“向量
”是“向量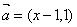 与向量
与向量 平行”的充分非必要条件; ③命题“
平行”的充分非必要条件; ③命题“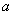 、
、 都是有理数”的否定是“
都是有理数”的否定是“ 的最小值等于
的最小值等于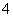 。其中正确结论的个数为
。其中正确结论的个数为