题目内容
 在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠ABC=90°,D为
在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠ABC=90°,D为棱BB1中点.
(Ⅰ)求证:面DA1C⊥面AA1C1 C;
(Ⅱ)设AB=BC=AA1=2,求B1到平面A1DC的距离.
考点:点、线、面间的距离计算,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出EF
DB,DE∥BF,从而得到DE⊥平面A1C1AC,由此能够证明面DA1C⊥面AA1C1C.
(Ⅱ)设B1到平面A1DC的距离为h.由VB1-A1DC=VC-A1B1D,利用等积法能求出B1到平面A1DC的距离.
| ∥ |
. |
(Ⅱ)设B1到平面A1DC的距离为h.由VB1-A1DC=VC-A1B1D,利用等积法能求出B1到平面A1DC的距离.
解答:
(Ⅰ)证明:设E是A1C的中点,F是AC的中点,
连结DE,BF,EF,
则EF
AA1,
∵在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,
∠ABC=90°,D为棱BB1中点,
∴DB
AA1,∴EF
DB,∴DE∥BF,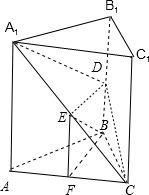
∵BF⊥平面A1C1AC,∴DE⊥平面A1C1AC,
∵DE?平面DA1C,∴面DA1C⊥面AA1C1C.
(Ⅱ)解:设B1到平面A1DC的距离为h.
∵VB1-A1DC=VC-A1B1D,AB=BC=AA1=2,
∴VC-A1B1D=
S△A1B1D•BC=
,
VB1-A1DC=
S△A1DC•h=
,
S△A1DC=
A1C•DE=
,
∴
S△A1DC•h=
,解得h=
,
∴B1到平面A1DC的距离为
.
连结DE,BF,EF,
则EF
| ∥ |
. |
| 1 |
| 2 |
∵在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,
∠ABC=90°,D为棱BB1中点,
∴DB
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |

∵BF⊥平面A1C1AC,∴DE⊥平面A1C1AC,
∵DE?平面DA1C,∴面DA1C⊥面AA1C1C.
(Ⅱ)解:设B1到平面A1DC的距离为h.
∵VB1-A1DC=VC-A1B1D,AB=BC=AA1=2,
∴VC-A1B1D=
| 1 |
| 3 |
| 2 |
| 3 |
VB1-A1DC=
| 1 |
| 3 |
| 2 |
| 3 |
S△A1DC=
| 1 |
| 2 |
| 6 |
∴
| 1 |
| 3 |
| 2 |
| 3 |
| ||
| 3 |
∴B1到平面A1DC的距离为
| ||
| 3 |
点评:本题考查平面垂直于平面的证明,考查点到平面的距离的求法,解题时要认真审题,注意等积法的合理运用.

练习册系列答案
相关题目
 执行如图所示的程序框图.则输出的所有点(x,y)都在函数( )的图象上.
执行如图所示的程序框图.则输出的所有点(x,y)都在函数( )的图象上.| A、y=x+1 |
| B、y=2x |
| C、y=2x |
| D、y=2x-1 |
已知p={x|y=
},Q={y|y=-x2+2x+1,x∈N},则P∩Q=( )
| x+1 |
| A、{1,2} |
| B、{x|-1≤x≤2} |
| C、{0,1,2} |
| D、∅ |
 已知正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面中心得三棱锥)
已知正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面中心得三棱锥)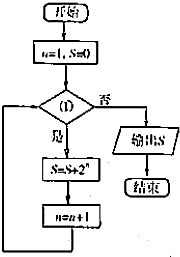 运行如图框图输出的S是254,则①应为
运行如图框图输出的S是254,则①应为