Question

4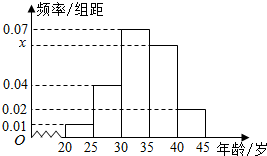．为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者，从符合条件的1000名志愿者中随机抽取100名志愿者，其中年龄频率分布直方图如图所示，其中x=3y，且年龄分组区间为：[[20，25]，[25，30），[30，35），[35，40），[40，45]．
（1）求x，y的值并根据频率分布直方图估计这1000名志愿者中年龄在[30，40）岁的人数；
（2）从这1000名志愿者中任选2名，记这2名志愿者则“年龄低于35岁”的人数为X，试以给出的频率分布直方图求得的频率作为概率求出X的分布列及数学期望．

Answer 1

分析 （1）由频率分布直方图中小矩形有面积等于频率及x=3y，能求出x，y的值；求出这1000名志愿者中年龄在[30，40）岁的频率，由此能估计这1000名志愿者中年龄在[30，40）岁的人数．
（2）X的可能取值为0，1，2，X～B（2，0.6），由此能求出X的分布列和EX．

解答 解：（1）∵频率分布直方图中小矩形有面积等于频率，
∴x+y=$\frac{1-（0.01+0.04+0.07）×5}{5}$=0.08，
又x=3y，解得x=0.06，y=0.02，
∴估计这1000名志愿者中年龄在[30，40）岁的人数为：
（0.07+0.06）×5×1000=650．
（2）由频率分布直方图得“年龄低于35岁”的频率为：
（0.01+0.04+0.07）×5=0.6，
则由题意知“年龄低于35岁”的概率为0.6，
∴X的可能取值为0，1，2，X～B（2，0.6），
P（X=0）=（1-0.6）²=0.16，
P（X=1）=${C}_{2}^{1}×0.6×（1-0.6）=0.48$，
P（X=2）=0.6²=0.36，
∴X的分布列为：

X	0	1	2
P	0.16	0.48	0.36

EX=0×0.16+1×0.48+2×0.36=1.2．

点评 本题考查频率分布直方图的应用，考查离散型随机变量的分布列及数学期望的求法，是中档题，解题时要认真审题，注意二项分布的合理运用．