题目内容
11.△ABC内接于半径为2的圆O,且3$\overrightarrow{OA}$+2$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$.(1)分别求出△ABC三条边的长;
(2)若M是线段AC的中点,点P在线段MC上运动,$\overrightarrow{BQ}$=$\frac{1}{3}$$\overrightarrow{QC}$,求$\overrightarrow{BP}$•$\overrightarrow{AQ}$的取值范围.
分析 (1)由3$\overrightarrow{OA}$+2$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$得-3$\overrightarrow{OA}$=2$\overrightarrow{OB}$+4$\overrightarrow{OC}$,两边平方解出$\overrightarrow{OB}•\overrightarrow{OC}$,代入夹角公式求出cos∠BOC,再利用余弦定理求出BC,同理求出AB,AC;
(2)建立平面直角坐标系,写出各向量的坐标,代入数量积公式得出$\overrightarrow{BP}$•$\overrightarrow{AQ}$,求出新函数的值域.
解答  解:(1)|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=2,∵3$\overrightarrow{OA}$+2$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,∴-3$\overrightarrow{OA}$=2$\overrightarrow{OB}$+4$\overrightarrow{OC}$,∴9$\overrightarrow{OA}$2=4$\overrightarrow{OB}$2+16$\overrightarrow{OC}$2+16$\overrightarrow{OB}$$•\overrightarrow{OC}$,即36=16+64+16$\overrightarrow{OB}•\overrightarrow{OC}$,∴$\overrightarrow{OB}•\overrightarrow{OC}$=-$\frac{11}{4}$.
解:(1)|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=2,∵3$\overrightarrow{OA}$+2$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,∴-3$\overrightarrow{OA}$=2$\overrightarrow{OB}$+4$\overrightarrow{OC}$,∴9$\overrightarrow{OA}$2=4$\overrightarrow{OB}$2+16$\overrightarrow{OC}$2+16$\overrightarrow{OB}$$•\overrightarrow{OC}$,即36=16+64+16$\overrightarrow{OB}•\overrightarrow{OC}$,∴$\overrightarrow{OB}•\overrightarrow{OC}$=-$\frac{11}{4}$.
同理:$\overrightarrow{OA}•\overrightarrow{OB}$=1,$\overrightarrow{OA}•\overrightarrow{OC}$=-$\frac{7}{2}$.
∴cos∠BOC=$\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}|•|\overrightarrow{OC}|}$=-$\frac{11}{16}$,cos∠AOC=$\frac{\overrightarrow{OA}•\overrightarrow{OC}}{|\overrightarrow{OA}|•|\overrightarrow{OC}|}$=-$\frac{7}{8}$,cos∠AOB=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$=$\frac{1}{4}$.
在△AOB中,由余弦定理可得AB2=OA2+OB2-2OA•OB•cos∠AOB=6,∴AB=$\sqrt{6}$.
同理可得:BC=$\frac{3\sqrt{6}}{2}$,AC=$\sqrt{15}$.
(2)以OAx轴以O为原点建立平面直角坐标系,则A(2,0),B($\frac{1}{2}$,$\frac{\sqrt{15}}{2}$),C(-$\frac{7}{4}$,-$\frac{\sqrt{15}}{4}$).
∴Q(-$\frac{1}{16}$,$\frac{5\sqrt{15}}{16}$).∴$\overrightarrow{AQ}$=(-$\frac{33}{16}$,$\frac{5\sqrt{15}}{16}$),$\overrightarrow{BC}$=(-$\frac{9}{4}$,-$\frac{3\sqrt{15}}{4}$),$\overrightarrow{CA}$=($\frac{15}{4}$,$\frac{\sqrt{15}}{4}$).
设$\overrightarrow{CP}$=λ$\overrightarrow{CA}$=($\frac{15λ}{4}$,$\frac{\sqrt{15}λ}{4}$)(0≤λ$≤\frac{1}{2}$).则$\overrightarrow{BP}$=$\overrightarrow{BC}$+$\overrightarrow{CP}$=($\frac{15λ-9}{4}$,$\frac{\sqrt{15}λ-3\sqrt{15}}{4}$).
∴$\overrightarrow{BP}$•$\overrightarrow{AQ}$=$\frac{297-495λ}{64}$+$\frac{75λ-225}{64}$=-$\frac{105}{16}$λ+$\frac{9}{8}$.
∴当λ=0时,$\overrightarrow{BP}$•$\overrightarrow{AQ}$取得最大值$\frac{9}{8}$,当λ=$\frac{1}{2}$时,$\overrightarrow{BP}$•$\overrightarrow{AQ}$取得最小值-$\frac{69}{32}$.
∴$\overrightarrow{BP}$•$\overrightarrow{AQ}$的取值范围是[-$\frac{69}{32}$,$\frac{9}{8}$].
点评 本题考查了平面向量的数量积运算,建立平面直角坐标系利用坐标进行计算是常用方法,属于中档题.

| A. | [0,1) | B. | (0,1) | C. | (0,1] | D. | [0,1] |

| A. | 9 | B. | 12 | C. | 8 | D. | 10 |
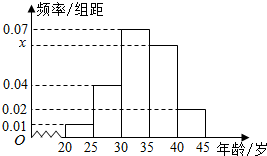 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的1000名志愿者中随机抽取100名志愿者,其中年龄频率分布直方图如图所示,其中x=3y,且年龄分组区间为:[[20,25],[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的1000名志愿者中随机抽取100名志愿者,其中年龄频率分布直方图如图所示,其中x=3y,且年龄分组区间为:[[20,25],[25,30),[30,35),[35,40),[40,45].