题目内容
18.函数y=a${\;}^{(3x-{x}^{2})}$(a>0)的递增区间是当0<a<1时,复合函数y=a${\;}^{(3x-{x}^{2})}$在(-∞,$\frac{3}{2}$]上为减函数;当a>1时,复合函数y=a${\;}^{(3x-{x}^{2})}$在($\frac{3}{2}$,+∞)上为增函数.分析 求出内函数的单调区间,然后对a分类,利用复合函数的单调性得答案.
解答 解:令t=3x-x2=-x2+3x,
对称轴方程为x=$\frac{3}{2}$,
当x∈(-∞,$\frac{3}{2}$]时,函数t=-x2+3x为增函数,
当x∈($\frac{3}{2},+∞$)时,函数t=-x2+3x为减函数,
∴当0<a<1时,复合函数y=a${\;}^{(3x-{x}^{2})}$在(-∞,$\frac{3}{2}$]上为减函数;
当a>1时,复合函数y=a${\;}^{(3x-{x}^{2})}$在($\frac{3}{2}$,+∞)上为增函数.
故答案为:当0<a<1时,复合函数y=a${\;}^{(3x-{x}^{2})}$在(-∞,$\frac{3}{2}$]上为减函数;
当a>1时,复合函数y=a${\;}^{(3x-{x}^{2})}$在($\frac{3}{2}$,+∞)上为增函数.
点评 本题考查复合函数的单调性,复合的两个函数同增则增,同减则增,一增一减则减,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.α锐角,直线$\left\{\begin{array}{l}x=1+tcos(α+\frac{3π}{2})\\ y=2+tsin(α+\frac{3π}{2})\end{array}\right.$(t为参数)的倾斜角是( )
| A. | α | B. | α-$\frac{π}{2}$ | C. | α+$\frac{π}{2}$ | D. | α+$\frac{3π}{2}$ |
9.方程|y+1|=x表示的曲线是( )
| A. |  | B. |  | C. |  | D. |  |
6.已知函数f(x-1)的定义域为[1,+∞),则函数F(x)=f($\frac{1}{x}$)+f(x-x2)的定义域为( )
| A. | [0,1) | B. | (0,1) | C. | (0,1] | D. | [0,1] |
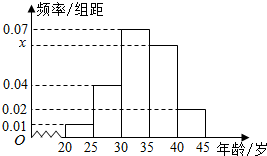 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的1000名志愿者中随机抽取100名志愿者,其中年龄频率分布直方图如图所示,其中x=3y,且年龄分组区间为:[[20,25],[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的1000名志愿者中随机抽取100名志愿者,其中年龄频率分布直方图如图所示,其中x=3y,且年龄分组区间为:[[20,25],[25,30),[30,35),[35,40),[40,45]. 如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,求异面直线AB1和BM所成的角的大小.(以B为坐标原点,BC为x轴,BB1为z轴,建立空间直角坐标系,利用空间向量求解)
如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,求异面直线AB1和BM所成的角的大小.(以B为坐标原点,BC为x轴,BB1为z轴,建立空间直角坐标系,利用空间向量求解)